题目内容
1. 如图所示,“
如图所示,“ ”型木块固定在地面上,木块水平表面AB粗糙,光滑表面BC且与水平面夹角为θ=37°.B点是弧形连接.一个质量为1kg的滑块从C点由静止开始下滑,经过1s时间达到B点.又经过2s时间停在A点.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
”型木块固定在地面上,木块水平表面AB粗糙,光滑表面BC且与水平面夹角为θ=37°.B点是弧形连接.一个质量为1kg的滑块从C点由静止开始下滑,经过1s时间达到B点.又经过2s时间停在A点.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:(1)斜面BC的长度;
(2)运动过程中滑块克服摩擦力做的功.
分析 (1)当滑块沿斜面BC向下运动时,滑块对斜面有斜向右下方的压力,则力传感器受到压力.由图读出滑块运动的时间为t=1s,由牛顿第二定律求出滑块的加速度,即可由位移公式求解斜面BC的长度.
(2)根据动能定理研究整个过程求解运动过程中滑块克服摩擦力做的功.
解答 解:(1)分析滑块受力,如图
由牛顿第二定律得:
得:a1=gsinθ=6m/s2
通过图象可知滑块在斜面上运动时间为:t1=1s
由运动学公式得:L=$\frac{1}{2}$a1t12=3m
(2)根据动能定理研究整个过程得
mgh+Wf=0-0
Wf=-18J,即运动过程中滑块克服摩擦力做的功是18J.
答:(1)斜面BC的长度是3m;
(2)运动过程中滑块克服摩擦力做的功是18J.
点评 分析滑块的受力情况和运动情况,关键要抓住牛顿第二定律和运动学公式的结合,掌握动能定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则他所受的合力大小为( )
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则他所受的合力大小为( )
 如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则他所受的合力大小为( )
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G,则他所受的合力大小为( )| A. | G | B. | Gsinθ | C. | Gcosθ | D. | 0 |
13. 如图所示,用F=20N的水平压力将一重为8N的木块紧压在竖直墙上,木块与墙面间的动摩擦因数为0.30.现木块施加一平行于墙面的拉力作用,使木块沿水平方向在墙面上以v=2m/s的速度向右匀速运动,则所施加的拉力大小为( )
如图所示,用F=20N的水平压力将一重为8N的木块紧压在竖直墙上,木块与墙面间的动摩擦因数为0.30.现木块施加一平行于墙面的拉力作用,使木块沿水平方向在墙面上以v=2m/s的速度向右匀速运动,则所施加的拉力大小为( )
 如图所示,用F=20N的水平压力将一重为8N的木块紧压在竖直墙上,木块与墙面间的动摩擦因数为0.30.现木块施加一平行于墙面的拉力作用,使木块沿水平方向在墙面上以v=2m/s的速度向右匀速运动,则所施加的拉力大小为( )
如图所示,用F=20N的水平压力将一重为8N的木块紧压在竖直墙上,木块与墙面间的动摩擦因数为0.30.现木块施加一平行于墙面的拉力作用,使木块沿水平方向在墙面上以v=2m/s的速度向右匀速运动,则所施加的拉力大小为( )| A. | 2.4N | B. | 6N | C. | 8N | D. | 10N |
16. 用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )
用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )
 用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )
用一水平拉力使质量为m的物体从静止开始沿粗糙的水平面运动,物体的v-t图象如图所示.下列表述正确的是( )| A. | 在0-t1时间内拉力逐惭减少到零 | B. | 在0-t1时间内物体做曲线运动 | ||
| C. | 在t1-t2时间内拉力的功率不为零 | D. | 在t1-t2时间内合外力做功$\frac{1}{2}$mv2 |
6. 如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
 如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )
如图所示,两个等量异种点电荷对称地放在一无限大平面的两侧(两点电荷未画出),O点是两点电荷连线与平面的交点,也是连线的中点.在平面内以O点为圆心画两个同心圆,两圆上分别有a、b、c、d四个点,则以下说法正确的是( )| A. | 若某个检验电荷只在此电场的电场力作用下运动到c点和d点时,加速度大小一定相等 | |
| B. | a、c两点电场强度大小相等 | |
| C. | 带正电的检验电荷从a点在平面内移动到d点电势能一定减小 | |
| D. | 检验电荷可以仅在此电场的电场力作用下在此平面内做匀速圆周运动 |
13. 如图所示,在粗糙水平板上放一个物块,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则( )
如图所示,在粗糙水平板上放一个物块,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则( )
 如图所示,在粗糙水平板上放一个物块,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则( )
如图所示,在粗糙水平板上放一个物块,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则( )| A. | 物块始终受到两个力作用 | |
| B. | 只有在a、b、c、d四点,物块受到的合外力才指向圆心 | |
| C. | 从a到b,物体所受的摩擦力先增大后减小 | |
| D. | 从b到a,物块处于超重状态 |
10.关于分子运动,下列说法中正确的是( )
| A. | 布朗运动就是液体分子的热运动 | |
| B. | 如图所示,布朗运动图中不规则折线表示的是液体分子的运动轨迹 | |
| C. | 当分子间的距离变小时,分子间作用力可能减小,也可能增大 | |
| D. | 物体温度改变时,物体分子的平均动能不一定改变 |

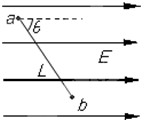 如图,匀强电场的场强为2×103V/m,a、b两点间的距离为0.1m,ab连线与电场方向的夹角为60°.求:
如图,匀强电场的场强为2×103V/m,a、b两点间的距离为0.1m,ab连线与电场方向的夹角为60°.求: