题目内容
19.在探究“加速度与力、质量的关系”的实验中,采用如图甲所示的装置.(1)某小组在探究“质量一定时,加速度与合外力成正比”的实验中,测出多组数据,作出了如图乙所示的图象,已知实验过程中细线与木板始终保持平行,则图线没有过坐标原点的原因可能是未平衡摩擦力,图线上部弯曲的原因可能是未满足砝码盘和砝码的总质量远小于木块的质量.

(2)如图丙所示,是使用频率为50Hz的打点计时器打出的一条纸带的一部分,0、1、2、3、4、5、6为依次选取的7个计数点,相邻两计数点间还有4个打点未画出.从纸带上测出x1=3.20cm,x2=4.52cm,x5=8.42cm,x6=9.70cm.则木块加速度的大小a=1.3m/s2(结果保留两位有效数字).
分析 (1)在“探究加速度a与物体所受合力F及质量m关系”的实验中,通过控制变量法,先控制m一定,验证a与F成正比,再控制F一定,验证a与m成反比;实验中用砂和砂桶的重力代替小车的合力,故要通过将长木板右端垫高来平衡摩擦力和使小车质量远大于砂和砂桶质量来减小实验的误差;
(2)利用逐差法(x5+x6)-(x1+x2)=8aT2求物体的加速度.
解答 解:(1)开始当小车挂上重物时,加速度却为零,线性图象不通过坐标原点,故导致图象不过原点的原因是木板倾角偏小.即说明操作过程中平衡摩擦力不足.
设小车的质量为M,砂和砂桶的质量为m,根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:a=$\frac{mg}{m+M}$
F拉=$\frac{Mmg}{m+M}$
当m<<M时,即当砝码和小桶的总重力要远小于小车的重力,绳子的拉力近似等于砂和砂桶的总重力.
从图象上可以看出:F从0开始增加,砂和砂桶的质量远小于车的质量,慢慢的砂和砂桶的重力在增加,那么在后面砂和砂桶的质量就没有远小于车的质量,由加速度表达式知a逐渐减小,所以图象向下弯曲.
所以原因是未满足砂和砂桶的质量远小于车的质量.
(2)由于相邻两计数点间还有4个打点未画出,故相邻两计数点间的时间间隔为T=5×0.02=0.1s..
应该利用逐差法求物体的加速度:(x5+x6)-(x1+x2)=8aT2
解得物体的加速度a=$\frac{{x}_{5}+{x}_{6}-{x}_{1}-{x}_{2}}{8{T}^{2}}=\frac{0.0842+0.0970-0.032-0.0452}{0.08}$=1.3m/s2
故答案为:(1)未平衡摩擦力;未满足砝码盘和砝码的总质量远小于木块的质量
(2)1.3
点评 解决本题的关键掌握纸带的处理,会通过纸带,运用匀变速直线运动的运动学公式,结合逐差法求解加速度,注意有效数字的保留.

 如图所示,某同学将空的薄金属筒开口向下压入水中,设水温均匀且恒定,筒内空气无泄漏,不计气体分子间相互作用,则被淹没的金属筒在缓慢下降过程中,筒内空气( )
如图所示,某同学将空的薄金属筒开口向下压入水中,设水温均匀且恒定,筒内空气无泄漏,不计气体分子间相互作用,则被淹没的金属筒在缓慢下降过程中,筒内空气( )| A. | 体积减小,内能减小 | B. | 体积增大,内能增大 | ||
| C. | 体积减小,向外界放热 | D. | 体积增大,从外界吸热 |
 模仿法拉第的实验(如图所示)
模仿法拉第的实验(如图所示)| 实验操作 | 实验现象(线圈B中有无电流) | 分析论证 |
| 开关闭合瞬间 | ①有 | 线圈B中磁场变化时,线圈B中有感应电流;线圈B中磁场不变时,线圈B中无感应电流 |
| 开关断开瞬间 | ②有 | |
| 开关保持闭合,滑动变阻器滑片不动 | ③无 | |
| 开关保持闭合,迅速移动滑动变阻器的滑片 | ④有 |
| A. | 跳高运动员起跳时,地对他的支持力大于他对地的压力 | |
| B. | 火箭加速上升时,火箭发动机产生的推力大于火箭自身的重力 | |
| C. | 鸡蛋撞击石头,鸡蛋破碎,鸡蛋对石头的作用力小于石头对鸡蛋的作用力 | |
| D. | 钢丝绳吊起货物加速上升时,钢丝绳对货物的拉力大于货物对钢丝绳的拉力 |
| A. | 所有行星绕太阳运动的轨道都是圆 | |
| B. | 所有行星绕太阳公转的周期都相同 | |
| C. | 太阳与行星间引力的方向沿着二者的连线 | |
| D. | 太阳对行星的引力大于行星对太阳的引力 |
| A. | 2F | B. | $\frac{F}{4}$ | C. | $\frac{F}{8}$ | D. | $\frac{F}{2}$ |
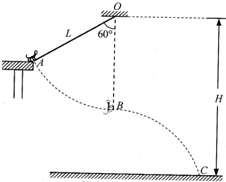 “猴子荡秋千”是马戏团的经典表演节目.如图所示,离地面高H=5.4m的O点固定一根长L=3.6m且不可伸长的轻质绳,在绳的一侧有一平台,拉直绳子,其末端正好位于平台边缘A点,绳子与竖直方向成60°角.有一质量m=5kg的猴子在A点抓住绳子末端无初速度地离开平台.在运动过程中猴子可视为质点,空气阻力不计,取g=10m/s2.求:
“猴子荡秋千”是马戏团的经典表演节目.如图所示,离地面高H=5.4m的O点固定一根长L=3.6m且不可伸长的轻质绳,在绳的一侧有一平台,拉直绳子,其末端正好位于平台边缘A点,绳子与竖直方向成60°角.有一质量m=5kg的猴子在A点抓住绳子末端无初速度地离开平台.在运动过程中猴子可视为质点,空气阻力不计,取g=10m/s2.求: 把一个质量为m=0.lkg的小球用细线悬挂起来,让小球在竖直平面内摆动,摆动中小球最高位置与最低位置的高度差为h=1.25m.不计阻力,取重力加速度g=10m/s2.在小球从最高位置摆到最低位置的过程中,问:
把一个质量为m=0.lkg的小球用细线悬挂起来,让小球在竖直平面内摆动,摆动中小球最高位置与最低位置的高度差为h=1.25m.不计阻力,取重力加速度g=10m/s2.在小球从最高位置摆到最低位置的过程中,问: