题目内容
7. 如图甲所示,长为L的平板车,质量为M=10kg,上表面到光滑水平地面的高度为h=1.25m,以速度v0=7.2m/s向右做匀速直线运动,A、B是其左右两个端点.从某时刻t=0起对平板车施加一个水平向左的恒力F,与此同时,将一个质量为m=1kg的小物块轻放在平板车上的P点(小物块可视为质点,放在P点时相对于地面的速度为零),PB=2m,经过一段时间,小物块脱离平板车落到地面.已知自t=0起到小物块脱离平板车止小物块和平板车的速度随时间变化的图线分别如图乙中的a和b(取水平向右为正方向),小物块下落过程中不会和平板车相碰,重力加速度为g=10m/s2.求:
如图甲所示,长为L的平板车,质量为M=10kg,上表面到光滑水平地面的高度为h=1.25m,以速度v0=7.2m/s向右做匀速直线运动,A、B是其左右两个端点.从某时刻t=0起对平板车施加一个水平向左的恒力F,与此同时,将一个质量为m=1kg的小物块轻放在平板车上的P点(小物块可视为质点,放在P点时相对于地面的速度为零),PB=2m,经过一段时间,小物块脱离平板车落到地面.已知自t=0起到小物块脱离平板车止小物块和平板车的速度随时间变化的图线分别如图乙中的a和b(取水平向右为正方向),小物块下落过程中不会和平板车相碰,重力加速度为g=10m/s2.求:(1)小物块与平板车间的动摩擦因数μ和恒力F分别多大?
(2)判断小物块从哪一端离开平板车?平板车长L至少多大?从t=0时起,平板车向右运动的最大距离s2m;
(3)自t=0时起到小物块脱离平板车止系统摩擦生热Q以及小物块落地时离平板车B端的水平距离x.
(s2m和x计算结果均保留三位有效数字)
分析 (1)由图象乙可知,在0~1s内,小物块向右做匀加速运动,平板车向右做匀减速运动,根据图象的斜率求出加速度,再根据牛顿第二定律求解即可;
(2)小物块将从B端离开平板车,根据运动学基本公式求解小车的最小长度,在1~3s内,小物块和平板车均向右做匀减速运动,根据图象求出平板车加速度,再根据运动学基本公式求解;
(3)先求出小物块相对平板车的运动路程,根据Q=μmg△s求出产生的热量,小物块离开平板车后,根据牛顿第二定律求出加速度,小物块离开车子做平抛运动,根据平抛运动基本公式结合位移关系求解.
解答 解:(1)由图象乙可知,在0~1s内,小物块向右做匀加速运动,平板车向右做匀减速运动,加速度大小分别为:a11=$\frac{△{v}_{11}}{△{t}_{1}}$=2m/s2和a21=$\frac{△{v}_{21}}{△{t}_{1}}=5.2m/{s}^{2}$,
分别对小物块和平板车受力分析,由牛顿运动定律有:
μmg=ma11
代入数据解得:μ=0.2
F+μmg=ma21,
代入数据解得:F=50N
(2)小物块将从B端离开平板车,由运动学公式并代入△t1=1s,v=2m/s有:
${s}_{21}=\frac{{v}_{0}+v}{2}△{t}_{1}=4.6m$,
${s}_{11}=\frac{v}{2}△{t}_{1}=1m$
可见,平板车长至少为:L=s21-s11+2m=5.6m
在1~3s内,小物块和平板车均向右做匀减速运动,平板车加速度大小为:a22=$\frac{△{v}_{22}}{△{t}_{2}}=4.8m/{s}^{2}$
从t=0时起,平板车向右运动的最大距离为:
${s}_{2m}={s}_{21}+\frac{{v}^{2}}{2{a}_{22}}=5.02m$
(3)由图象乙可知,小物块从t=0时起到离开平板车时所经历的时间为:t=△t1+△t2=3s
这段时间内小物块相对平板车的运动路程为:△s=2(s21-s11)+2m=9.2m
系统摩擦生热为:Q=μmg△s=18.4J
小物块刚离开平板车时,小车向左的速度大小为:v2=7.6m/s
小物块向左的速度大小为:v3=2m/s
小物块离开平板车后,车的加速度大小为:a23=$\frac{F}{M}$=5m/s2
小物块离开车子做平抛运动,有:h=$\frac{1}{2}$gt32,t3=0.5s
s13=v3t3=1m
车子在t3时间内向左运动的距离为:s23=v2t3+$\frac{1}{2}$a23t32=4.43m
所以,小物块落地时,离平板车B端的水平距离为:x=s23-s13=3.43m
答:(1)小物块与平板车间的动摩擦因数μ为0.2,恒力F为50N;
(2)判断小物块从B端离开平板车,平板车长L至为5.6m,从t=0时起,平板车向右运动的最大距离s2m为5.02m;
(3)自t=0时起到小物块脱离平板车止系统摩擦生热Q为18.4J,小物块落地时离平板车B端的水平距离x为3.43m.
点评 本题主要考查了牛顿第二定律、平抛运动基本公式以及匀变速直线运动基本公式的直接应用,解题的关键是根据速度时间图象的斜率表示加速度求解加速度,判断物体和小车的运动情况,难度较大,属于难题.


| A. | 甲图法拉第是英国著名物理学家,他提出了电场的观点,同时引入电场线直观描述电场 | |
| B. | 乙图中通过圆盘的磁通量保持不变,没有电流流经电阻R | |
| C. | 丙图实验中,如果将通电直导线东西方向放置,实验效果最好 | |
| D. | 丁图中阴极射线在磁场的作用下向上偏转 |
 图(甲)为某同学利用半圆形玻璃砖测定玻璃折射率n的装置示意图.他让光从空气射向玻璃砖,在正确操作后,他利用测出的数据作出了图(乙)所示的折射角正弦(sinr)与入射角正弦(sini)的关系图象.则下列说法正确的是( )
图(甲)为某同学利用半圆形玻璃砖测定玻璃折射率n的装置示意图.他让光从空气射向玻璃砖,在正确操作后,他利用测出的数据作出了图(乙)所示的折射角正弦(sinr)与入射角正弦(sini)的关系图象.则下列说法正确的是( )| A. | 该玻璃的折射率n=$\frac{2}{3}$ | |
| B. | 该玻璃的折射率n=1.5 | |
| C. | 光由空气进入该玻璃砖中传播时,光波频率变为原来的$\frac{2}{3}$倍 | |
| D. | 光由空气进入该玻璃砖中传播时,光波波长变为原来的1.5倍 |

| A. | 当地重力加速度为$\frac{c}{2s}$ | |
| B. | 当v2=c时,物块一定处于完全失重状态 | |
| C. | 物体的质量m=$\frac{2b}{cs}$ | |
| D. | a=2b |
| A. | 温度是描述物体的冷热程度的状态量 | |
| B. | 温度是热平衡系统具有“共同性质”的物理量 | |
| C. | 温度是决定一个系统与另一个系统是否达到热平衡状态的物理量 | |
| D. | 只有两个系统的温度、体积、压强均相同,这两个系统才达到了热平衡状态 |
 如图所示是研究光电效应的电路,阴极K和阳极A是密封在真空玻璃管中的两个电极,K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法不正确的是 ( )
如图所示是研究光电效应的电路,阴极K和阳极A是密封在真空玻璃管中的两个电极,K在受到光照时能够发射光电子.阳极A吸收阴极K发出的光电子,在电路中形成电流.如果用单色光a照射阴极K,电流表的指针发生偏转;用单色光b照射光电管阴极K时,电流表的指针不发生偏转.下列说法不正确的是 ( )| A. | a光的波长一定小于b光的波长 | |
| B. | 只增加a光的强度可能使通过电流表的电流增大 | |
| C. | 只增加a光的强度可使逸出的电子最大初动能变大 | |
| D. | 用单色光a照射阴极K,当电源的正、负极对调时,电流表的读数可能减为零 |
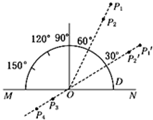 如图所示,一半圆形玻璃砖外面插上P1、P2、P3、P4四枚大头针时,P3、P4恰可挡住P1、P2所成的像.有一同学把大头针插在P1′和P2′位置时,在MN另外一侧看不到大头针的像.其原因是光线在玻璃砖内发生了全反射.
如图所示,一半圆形玻璃砖外面插上P1、P2、P3、P4四枚大头针时,P3、P4恰可挡住P1、P2所成的像.有一同学把大头针插在P1′和P2′位置时,在MN另外一侧看不到大头针的像.其原因是光线在玻璃砖内发生了全反射. 如图所示,半圆形玻璃砖的半径R=10cm,直径AB与屏幕垂直并接触于A点,激光束a垂直AB射向半圆形玻璃砖的圆心O,以O点为轴,从图示位置在纸面内沿顺时针方向旋转.当转过角度为30°时,光屏上有两个光斑,当转过角度刚好为45°时,光屏上恰好只有一个光斑.求:
如图所示,半圆形玻璃砖的半径R=10cm,直径AB与屏幕垂直并接触于A点,激光束a垂直AB射向半圆形玻璃砖的圆心O,以O点为轴,从图示位置在纸面内沿顺时针方向旋转.当转过角度为30°时,光屏上有两个光斑,当转过角度刚好为45°时,光屏上恰好只有一个光斑.求: