题目内容
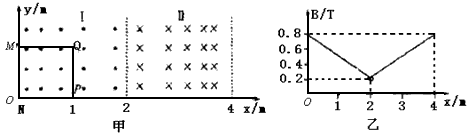
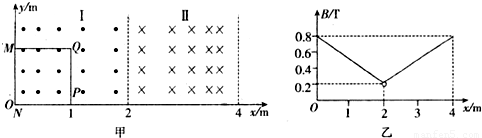
如图甲,一边长为L=lm、电阻为R=3Ω的正方形金属线框MNPQ水平平放在光滑绝缘水平地面上,在地面上建立如图所示坐标系,空间存在垂直地面的磁场,在0≤x<2m的区域I中磁场方向向上,在2<x≤4m 的区域Ⅱ中磁场方向向下,磁感应强度的大小随x的变化规律如图乙,开始时刻线框MN边与y轴重合.

(1)若给线框以水平向右的初速度,同时在PQ边施加一水平拉力,之后线框做v=1m/s 的匀速直线运动,求第2秒内水平拉力做的功;
(2)若I、Ⅱ区域中的磁场均为磁感应强度为B=0.8T的匀强磁场,方向仍如图甲,现在图示位置给线框一初速度,线框MN边运动到磁场区域Ⅱ的右边界时速度恰为零,设线框从MN边在区域I中运动时线框中产生的热量Q1,线框MN边在区域Ⅱ中运动时线框中产生的热量为Q2,求
.

(1)若给线框以水平向右的初速度,同时在PQ边施加一水平拉力,之后线框做v=1m/s 的匀速直线运动,求第2秒内水平拉力做的功;
(2)若I、Ⅱ区域中的磁场均为磁感应强度为B=0.8T的匀强磁场,方向仍如图甲,现在图示位置给线框一初速度,线框MN边运动到磁场区域Ⅱ的右边界时速度恰为零,设线框从MN边在区域I中运动时线框中产生的热量Q1,线框MN边在区域Ⅱ中运动时线框中产生的热量为Q2,求
| Q1 | Q2 |
分析:(1)用法拉第电磁感应定律求出回路中的电动势,水平拉力做的功等于线框中产生的焦耳热;
(2)线框匀速运动一段时间后减速,MN边到达中间界线时速度为v1,接着又匀速运动一段时间后,再减速,最后速度为0,对跨越边界的过程据动量定理和法拉第电磁感应定律与电量的计算公式:q=
△t,最后取得Q1和Q2的关系公式.
(2)线框匀速运动一段时间后减速,MN边到达中间界线时速度为v1,接着又匀速运动一段时间后,再减速,最后速度为0,对跨越边界的过程据动量定理和法拉第电磁感应定律与电量的计算公式:q=
. |
| I |
解答:解:(1)PQ在区域Ⅱ中距中间边界△x,而MN在区域I 距中间边界L-△x时,PQ边产生的感应电动势:E1=(0.2+0.3x)Lv
MN边产生的感应电动势:E2=[0.2+0.3△x(L-△x)]Lv
代人数据解得回路中的电动势:E=E1+E2=0.7V
由于线框匀速运动,故水平拉力做的功等于线框中产生的焦耳热,即
W=Q=
t=0.163J
(2)设初速度为v0,匀速运动一段时间后减速,MN边到达中间界线时速度为v1,接着又匀速运动一段时间后,再减速,最后速度为0,则对跨越中间边界的过程据动量定理有
2BL
△t=2BLq1=mv0-mv1
对跨越最右边界的过程据动量定理有:BLq2=mv1-0
线圈运动时产生的平均感应电动势:
=
=
,电量q=
△t
联立化简得 q=
由上式可得:q1=2q2
则 v0=5v1
故:Q1=
m
-
m
Q2=
m
-0
则:
=24
答:(1)第2秒内水平拉力做的功W=0.163J;
(2 )
=24.
MN边产生的感应电动势:E2=[0.2+0.3△x(L-△x)]Lv
代人数据解得回路中的电动势:E=E1+E2=0.7V
由于线框匀速运动,故水平拉力做的功等于线框中产生的焦耳热,即
W=Q=
| E2 |
| R |
(2)设初速度为v0,匀速运动一段时间后减速,MN边到达中间界线时速度为v1,接着又匀速运动一段时间后,再减速,最后速度为0,则对跨越中间边界的过程据动量定理有
2BL
. |
| I |
对跨越最右边界的过程据动量定理有:BLq2=mv1-0
线圈运动时产生的平均感应电动势:
. |
| E |
| △Φ |
| △t |
. |
| I |
| ||
| R |
. |
| I |
联立化简得 q=
| △Φ |
| R |
由上式可得:q1=2q2
则 v0=5v1
故:Q1=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 1 |
Q2=
| 1 |
| 2 |
| v | 2 1 |
则:
| Q1 |
| Q2 |
答:(1)第2秒内水平拉力做的功W=0.163J;
(2 )
| Q1 |
| Q2 |
点评:考查楞次定律、法拉第电磁感应定律、闭合电路欧姆定律及焦耳定律等规律的应用,同时掌握图象在本题的应用

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

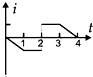
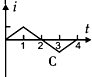
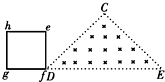 如图甲所示,在虚线所示的等腰直角三角形CDE(其底边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(gf边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度v匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图乙所示的四个i-t图象(横轴单位长度表示的值为L/v),哪一个能反映线框中感应电流的规律( )
如图甲所示,在虚线所示的等腰直角三角形CDE(其底边DE长为3L)区域内,存在有垂直纸面向里的匀强磁场,一边长为L的正方形线框efgh(gf边与DE边在同一直线上)在纸平面内沿DE方向从左向右以速度v匀速通过场区.若以图示位置为计时起点,规定逆时针方向为线框中感应电流的正方向,则图乙所示的四个i-t图象(横轴单位长度表示的值为L/v),哪一个能反映线框中感应电流的规律( )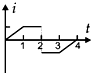
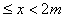 的区域Ⅰ中磁场方向向上,在
的区域Ⅰ中磁场方向向上,在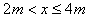 的区域Ⅱ中磁场方向向下,磁感应强度的大小随x的变化规律如图乙所示,开始时刻线框MN边与y轴重合。
的区域Ⅱ中磁场方向向下,磁感应强度的大小随x的变化规律如图乙所示,开始时刻线框MN边与y轴重合。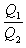 。
。 
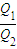 .
.