题目内容
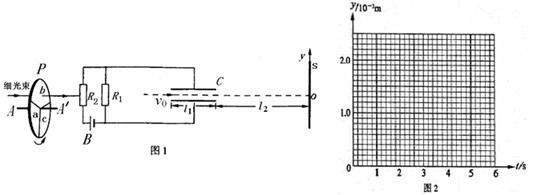
图1中B为电源,电动势![]() ,内阻不计。固定电阻
,内阻不计。固定电阻![]() ,R2为光敏电阻。C为平行板电容器,虚线到两极板距离相等,极板长
,R2为光敏电阻。C为平行板电容器,虚线到两极板距离相等,极板长![]() ,两极板的间距
,两极板的间距![]() 。S为屏,与极板垂直,到极板的距离
。S为屏,与极板垂直,到极板的距离![]() 。P为一圆盘,由形状相同、透光率不同的三个扇形a、b和c构成,它可绕
。P为一圆盘,由形状相同、透光率不同的三个扇形a、b和c构成,它可绕![]() 轴转动。当细光束通过扇形a、b、c照射光敏电阻R2时,R2的阻值分别为1000Ω、2000Ω、4500Ω。有一细电子束沿图中虚线以速度
轴转动。当细光束通过扇形a、b、c照射光敏电阻R2时,R2的阻值分别为1000Ω、2000Ω、4500Ω。有一细电子束沿图中虚线以速度![]() 连续不断地射入C。已知电子电量
连续不断地射入C。已知电子电量![]() ,电子,电子质量
,电子,电子质量![]() 。忽略细光束的宽度、电容器的充电放电时间及电子所受的重力。假设照在R2上的光强发生变化时R2阻值立即有相应的改变。
。忽略细光束的宽度、电容器的充电放电时间及电子所受的重力。假设照在R2上的光强发生变化时R2阻值立即有相应的改变。
(1)设圆盘不转动,细光束通过b照射到R2上,求电子到达屏S上时,它离O点的距离y。(计算结果保留二位有效数字)。
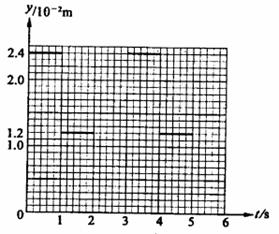
(2)设转盘按图1中箭头方向匀速转动,每3秒转一圈。取光束照在a、b分界处时t=0,试在图2给出的坐标纸上,画出电子到达屏S上时,它离O点的距离y随时间t的变化图线(0—6s间)。要求在y轴上标出图线最高点与最低点的值。(不要求写出计算过程,只按画出的图线评分。)
(1)设电容器C两板间的电压为U,电场强度大小为E,电子在极板间穿行时y方向上的加速度大小为a , 穿过C的时间为t1,穿出时电子偏转的距离为y1 ,
U=![]() E=
E=![]() eE=ma t1=
eE=ma t1=![]() y1=
y1=![]() at12
at12
由以上各式得y1=![]() (
(![]() )
)![]() 代人数据得 y1=4.8×10-3m
代人数据得 y1=4.8×10-3m
由此可见y1<![]() d,电子可通过C。
d,电子可通过C。
设电子从C穿出时,沿y 方向的速度为vy,穿出后到达屏S所经历的时间为t2,在此时间内电子在y 方向移动的距离为y2,
vy=at t2=![]() y2=vyt2
y2=vyt2
由以上有关各式得y2=![]() (
(![]() )
)![]() 代人数据得 y2=1.92×10-2m
代人数据得 y2=1.92×10-2m
由题意 y = y1+y2=2.4×10-2m 。
( 2 )如图所示。

 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案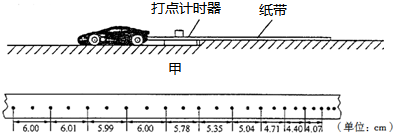 在上述过程中,打点计时器在纸带上所打的部分点迹如图乙所示.
在上述过程中,打点计时器在纸带上所打的部分点迹如图乙所示.
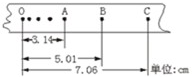 (2)在“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50HZ,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.甲、乙、丙三学生分别用同一装置打出三条纸带,量出各纸带上第1、2两点间的距离分别为0.12cm,0.19cm和0.25cm,可见操作上有错误的是学生
(2)在“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50HZ,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg.甲、乙、丙三学生分别用同一装置打出三条纸带,量出各纸带上第1、2两点间的距离分别为0.12cm,0.19cm和0.25cm,可见操作上有错误的是学生 (1)某同学用游标为20分度的卡尺测量一薄金属圆板的直径D,用螺旋测微器测量其厚度d,示数如图所示.由图可读出D=
(1)某同学用游标为20分度的卡尺测量一薄金属圆板的直径D,用螺旋测微器测量其厚度d,示数如图所示.由图可读出D=