题目内容
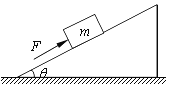
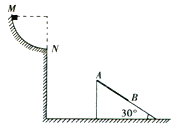
【题目】一表面光滑倾角为![]() 的斜面体固定在水平面上,在斜面体的上端用销钉固定一质量为
的斜面体固定在水平面上,在斜面体的上端用销钉固定一质量为![]() 的长木板
的长木板![]() ,且
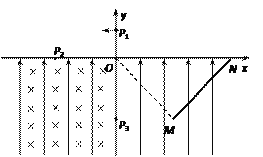
,且![]() 点到斜面体下端的间距足够长。斜面体的左侧某位置有一带有光滑的
点到斜面体下端的间距足够长。斜面体的左侧某位置有一带有光滑的![]() 圆弧轨道的平台,其中半径为
圆弧轨道的平台,其中半径为![]() 点与圆心等高,
点与圆心等高, ![]() 点的切线水平。现将一可视为质点的质量为
点的切线水平。现将一可视为质点的质量为![]() 的滑块由
的滑块由![]() 点无初速度释放,经过一段时间滑块无碰撞地滑上长木板,同时立即将销钉拔掉,使滑块和长木板具有共同的速度。已知滑块与长木板之间的动摩擦因数为
点无初速度释放,经过一段时间滑块无碰撞地滑上长木板,同时立即将销钉拔掉,使滑块和长木板具有共同的速度。已知滑块与长木板之间的动摩擦因数为![]() ,重力加速度
,重力加速度![]() 。试求:
。试求:
(1)滑块离开![]() 点前的瞬间对
点前的瞬间对![]() 点的压力;
点的压力;
(2)滑块由![]() 点运动到
点运动到![]() 点的时间;
点的时间;
(3)滑块与长木板的共同速度。
【答案】(1)3N(2)![]() (3)3.465m/s
(3)3.465m/s
【解析】(1)滑块从M点运动到N点的过程中机械能守恒,设滑块运动到N点时的速度为vB,则有: ![]()
解得![]() ,
,
带入数据可知vB=2m/s;
滑块到达N点,由牛顿定理: ![]() ,解得F=3N
,解得F=3N
则滑块到达N点对轨道的压力大小为3N.
(2)由于滑块无碰撞地滑上长木板,滑块离开N点后做平抛运动,设经过时间t1运动到A点,到达A点时的水平方向的分速度为vx,竖直分速度vy,则![]()
所以![]() 又vy=gt1,
又vy=gt1,
所以![]()
(3)滑块到达A点时的和速度: ![]()
到达A点后,此时滑块的加速度为a1,则沿斜面方向有:
![]() ,
,
解得a2=7.5m/s2方向沿斜面向下,
设经过时间t2两者速度相等,则:v+a1t2=a2t2,
联立带入数据解得:t2≈0.462s
二者的共同速度:v共=a2t2=3.465m/s

练习册系列答案
相关题目