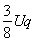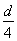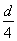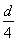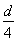题目内容
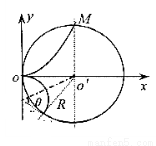
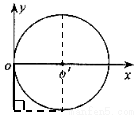
如图所示，xOy平面内半径为R的圆O'与y轴相切于原点O。在该圆区域内，有与y轴平行的匀强电场和垂直于圆面的匀强磁场。一质量为m、电荷量为q的粒子（不计重力）从O点沿x轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经T0时间从P点射出。
（1）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经
时间恰从圆形区域的边界射出。求电场强度的大小和粒子离开电场时速度的大小；
（2）若仅撤去电场，带电粒子仍从O点射入，且速度为原来的2倍，求粒子在磁场中运动的时间。
（1）E=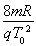
；
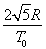；（2）
。
【解析】
试题分析：（1）设电场强度为E，磁感强度为B；粒子的初速度为v。同时存在电场和磁场时，带电粒子做匀速直线运动，有：2R=vT0；解得v=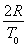
（1分）
撤去磁场，只存在电场时，粒子做类平抛运动，有：
x=v×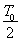
（1分） y=
×
（1分）
由以上式子可知x=y=R，粒子从图中的M点离开电场，解得：E=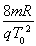
（1分）
又：vx=v，vy=at=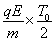
（1分）
则粒子离开电场时的速度V=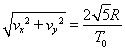
（1分）
（2）同时存在电场和磁场时，带电粒子做匀速直线运动有：qvB=qE （1分）
只存在磁场时，粒子做匀速圆周运动，设半径为r。
q×2v×B =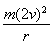
（1分）
由以上式子可求得r=R，可知粒子在磁场中运动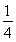
圆周 （2分）
所以，粒子在磁场中运动的时间t=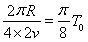
（2分）
考点：带电粒子在磁场与电场中的运动。
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
