题目内容
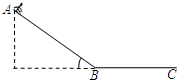 在某旅游景区,建有一山坡滑草运动项目.如图所示,设山坡AB可看成长度为L=50m、倾角θ=370的斜面,山坡低端与一段水平缓冲段BC圆滑连接.一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为?=0.25.他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段,再滑行一段距离后安全停下来. 不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
在某旅游景区,建有一山坡滑草运动项目.如图所示,设山坡AB可看成长度为L=50m、倾角θ=370的斜面,山坡低端与一段水平缓冲段BC圆滑连接.一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为?=0.25.他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段,再滑行一段距离后安全停下来. 不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)此游客滑到山坡底端时的速度大小;
(2)此游客从A点到B点的下滑过程中摩擦力对他做的功;
(3)此游客进入BC段后水平滑行的距离.
分析:(1)游客在山坡上做匀加速运动,根据牛顿第二定律求出游客在山坡上运动的加速度,由速度位移关系式求解游客滑到山坡底端时的速度大小;
(2)游客在山坡上受到滑动摩擦力为f=μmgcosθ,摩擦力对游客做负功,根据功的公式求出游客从A点到B点的下滑过程中摩擦力对他做的功;
(3)游客在水平面由于摩擦力而做匀减速运动,根据牛顿第二定律求出加速度,再由运动学公式求出游客进入BC段后水平滑行的距离.
(2)游客在山坡上受到滑动摩擦力为f=μmgcosθ,摩擦力对游客做负功,根据功的公式求出游客从A点到B点的下滑过程中摩擦力对他做的功;
(3)游客在水平面由于摩擦力而做匀减速运动,根据牛顿第二定律求出加速度,再由运动学公式求出游客进入BC段后水平滑行的距离.
解答:解:(1)设游客在山坡上滑行时加速度大小为a,游客滑到山坡底端时的速度大小为vB,则有:
根据牛顿第二定律得
ma=mgsinθ-μmgcosθ
得到a=gsinθ-μgcosθ=10×0.6-0.25×10×0.8=4m/s2
由
=2aL得:vB=
=
m/s=20m/s
(2)此游客从A点到B点的下滑过程中摩擦力对他做的功:Wf=-μmgcosθ?L=-8×103J
(3)设PB距离为x,游客在水平段滑行的加速度为
a/=
=μg=2.5m/s2
由
=2a/x,得x=
=80m
答:
(1)此游客滑到山坡底端时的速度大小为20m/s;
(2)此游客从A点到B点的下滑过程中摩擦力对他做的功-8×103J;
(3)此游客进入BC段后水平滑行的距离为80m.
根据牛顿第二定律得
ma=mgsinθ-μmgcosθ
得到a=gsinθ-μgcosθ=10×0.6-0.25×10×0.8=4m/s2
由
| v | 2 B |
| 2aL |
| 2×4×50 |
(2)此游客从A点到B点的下滑过程中摩擦力对他做的功:Wf=-μmgcosθ?L=-8×103J
(3)设PB距离为x,游客在水平段滑行的加速度为
a/=
| μmg |
| m |
由
| v | 2 B |
| ||
| 2a/ |
答:
(1)此游客滑到山坡底端时的速度大小为20m/s;
(2)此游客从A点到B点的下滑过程中摩擦力对他做的功-8×103J;
(3)此游客进入BC段后水平滑行的距离为80m.
点评:本题属于动力学中由受力情况确定运动情况的类型,运用牛顿定律和运动学结合求解的,也可以根据动能定理处理,更为简捷方便.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
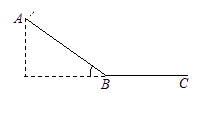 (3)此游客进入BC段后水平滑行的距离。
(3)此游客进入BC段后水平滑行的距离。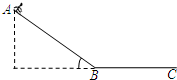
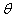 =37°的斜面,山坡低端与一段水平缓冲段BC圆滑连接。一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为μ=0.25。他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段,再滑行一段距离后安全停下来。不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8。求:
=37°的斜面,山坡低端与一段水平缓冲段BC圆滑连接。一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为μ=0.25。他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段,再滑行一段距离后安全停下来。不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8。求: 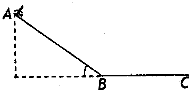
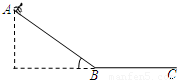 在某旅游景区,建有一山坡滑草运动项目.如图所示,设山坡AB可看成长度为L=50m、倾角θ=37的斜面,山坡低端与一段水平缓冲段BC圆滑连接.一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为µ=0.25.他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段,再滑行一段距离后安全停下来. 不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求:
在某旅游景区,建有一山坡滑草运动项目.如图所示,设山坡AB可看成长度为L=50m、倾角θ=37的斜面,山坡低端与一段水平缓冲段BC圆滑连接.一名游客连同滑草装置总质量m=80kg,滑草装置与AB段及BC段间动摩擦因数均为µ=0.25.他从A处由静止开始匀加速下滑,通过B点滑入水平缓冲段,再滑行一段距离后安全停下来. 不计空气阻力,取g=10m/s2,sin37°=0.6,cos37°=0.8.求: