题目内容
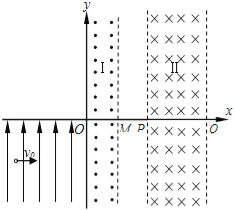
【题目】如图所示，两根相距为d的足够长的平行金属导轨位于水平xOy平面内，左端接有阻值为R的电阻，其他部分的电阻均不计。在x>0的一侧存在垂直xOy平面且方向竖直向下的磁场，磁感强度大小按B=kx规律变化（其中k是一大于零的常数）。一根质量为m的金属杆垂直跨搁在光滑的金属导轨上，两者接触良好。当t=0时直杆位于x=0处，其速度大小为v0，方向沿x轴正方向，在此后的过程中，始终有一个方向向左的变力F作用于金属杆，使金属杆的加速度大小恒为a，加速度方向一直沿x轴的负方向．求：
（1）金属杆向右运动至t=0时刻时所在位置处的磁感应强度B的大小。
（2）闭合回路中感应电流持续的时间有多长？
（3）当金属杆的速度为v0/2时，闭合回路的感应电动势多大？此时作用于金属杆的外力F多大？
【答案】（1）
（2）
（3）
； 
【解析】试题分析:（1）杆做匀变速直线运动，由位移公式可知：金属杆向右运动至t0时刻时的位移
，所以此时的磁感应强度
（2）杆先向右做匀减速运动，后向左做匀加速运动，最后会离开磁场，设t为在磁场区内向右做匀减速直线运动的时间，则v0-at=0，根据对称性可得：感应电流的持续时间：
（3）设x1为金属杆的速度大小为
时它所在的坐标，由速度位移关第
，解得
，此时回路中的感应电动势
当金属杆沿xl轴正方向运动时，由牛顿第二定律得：F+BdI=ma
由欧姆定律
解得外力
。
同理可以求出，当金属杆沿xl轴正方向运动时，外力
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
