题目内容
7.宇航员站在一个星球表面上的某高处h自由释放一小球,不计空气阻力,经过时间t落地,已知宇航员的质量为m,该星球的半径为R,引力常量为G,求解出该星球的质量M?分析 根据匀变速直线运动的位移时间公式求出星球表面的重力加速度,根据万有引力等于重力求出星球的质量.
解答 解:设星球表面重力加速度为g,由运动学得:
h=$\frac{1}{2}$gt2
解得:g=$\frac{2h}{{t}^{2}}$
由星球表面万有引力等于重力可得,
$\frac{GMm}{{R}^{2}}$=mg
解得:M=$\frac{2{hR}^{2}}{{Gt}^{2}}$
答:该星球的质量为$\frac{2{hR}^{2}}{{Gt}^{2}}$.
点评 解决本题的关键掌握万有引力等于重力这一理论,结合表面的重力加速度和天体的半径求解天体的质量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.跳高时要铺上厚厚的垫子,这是为了( )
| A. | 减少运动员受到的冲量? | B. | 减少运动员受到的冲力? | ||
| C. | 减少运动员的动量的变化? | D. | 减小运动员的惯性? |
15.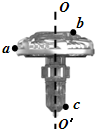 如图所示是小朋友中比较流行的陀螺游戏中的一种陀螺,a、b、c是陀螺上的三个点.当陀螺绕垂直于地面的轴线OO′以角速度ω稳定旋转时,下列表述正确的是( )
如图所示是小朋友中比较流行的陀螺游戏中的一种陀螺,a、b、c是陀螺上的三个点.当陀螺绕垂直于地面的轴线OO′以角速度ω稳定旋转时,下列表述正确的是( )
 如图所示是小朋友中比较流行的陀螺游戏中的一种陀螺,a、b、c是陀螺上的三个点.当陀螺绕垂直于地面的轴线OO′以角速度ω稳定旋转时,下列表述正确的是( )
如图所示是小朋友中比较流行的陀螺游戏中的一种陀螺,a、b、c是陀螺上的三个点.当陀螺绕垂直于地面的轴线OO′以角速度ω稳定旋转时,下列表述正确的是( )| A. | b和c两点的线速度大小相等 | B. | a和b两点的角速度相等 | ||
| C. | b点的角速度比c点的大 | D. | c点的线速度比a点的大 |
12.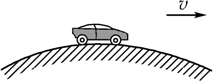 如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法不正确的是( )
如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法不正确的是( )
 如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法不正确的是( )
如图所示,汽车以一定的速度经过一个圆弧形桥面的顶点时,关于汽车的受力及汽车对桥面的压力情况,以下说法不正确的是( )| A. | 在竖直方向汽车可能只受重力 | |
| B. | 在竖直方向汽车可能只受两个力:重力和桥面的支持力 | |
| C. | 在竖直方向汽车受到三个力:重力、桥面的支持力和向心力 | |
| D. | 汽车对桥面的压力可能为0 |
19.在“碰撞中的动量守恒实验”中,实验必须要求的条件 ( )
| A. | 斜槽轨道必须光滑 | |
| B. | 斜槽轨道末端的切线必须水平 | |
| C. | 入射小球每次都要从同一高度由静止滚下 | |
| D. | 碰撞的瞬间,入射小球和被碰小球的球心连线与轨道末端的切线平行 |
 如图所示,在水平转盘上,距转动轴20cm处有一个质量为20g的小木块,当转盘的转动周期为2s时,木块与转盘之间没有相对滑动,问木块受几个力?每个力是多大?方向怎样?
如图所示,在水平转盘上,距转动轴20cm处有一个质量为20g的小木块,当转盘的转动周期为2s时,木块与转盘之间没有相对滑动,问木块受几个力?每个力是多大?方向怎样? 如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量为m=0.2kg的小球从外轨道的最低点A处以初速度v0向右运动,小球的直径略小于两圆的间距,小球运动的轨道半径R=0.2m,取g=10m/s2.
如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量为m=0.2kg的小球从外轨道的最低点A处以初速度v0向右运动,小球的直径略小于两圆的间距,小球运动的轨道半径R=0.2m,取g=10m/s2. 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度在A点冲上轨道,当小球将要从轨道口B点水平飞出时,对轨道的压力为小球重力的一半,则小球落地点C距半圆形轨道切入点A处有多远?
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度在A点冲上轨道,当小球将要从轨道口B点水平飞出时,对轨道的压力为小球重力的一半,则小球落地点C距半圆形轨道切入点A处有多远?