题目内容
【题目】如图所示,A、B为水平放置的间距d=0.2m的两块足够大的平行金属板,两板间有场强为E=0.1V/m、方向由B指向A的匀强电场.一喷枪从A、B板的中央点P向各个方向均匀地喷出初速度大小均为v0=10m/s的带电微粒.已知微粒的质量均为m=1.0×10﹣5kg、电荷量均为q=﹣1.0×10﹣3C,不计微粒间的相互作用及空气阻力的影响,取g=10m/s2 . 求:
(1)求从P点水平喷出的微粒打在极板时的水平位移x.
(2)要使所有微粒从P点喷出后均做直线运动,应将板间的电场调节为E′,求E′的大小和方向;在此情况下,从喷枪刚开始喷出微粒计时,求经t0=0.02s时两板上有微粒击中区域的面积和.
(3)在满足第(2)问中的所有微粒从P点喷出后均做直线运动情况下,在两板间加垂直于纸面向里的匀强磁场,磁感应强度B=1T.求B板被微粒打中的区域长度.
【答案】
(1)解:微粒在匀强电场做类平抛运动,微粒的加速度: ![]()
根据运动学: ![]()
得运动的半径为:x=v0t
解得:x=1m
答:从P点水平喷出的微粒打在极板时的水平位移x.
(2)解:要使微粒做直线,电场应反向,且有:qE'=mg ![]()
故电场应该调节为方向向下,大小为:E'=0.1V/m
经t0=0.02s时,微粒运动的位移为:s=v0t
极板上被微粒击中区域为半径为r的圆,其中 ![]() S=2πr2=0.06πm2
S=2πr2=0.06πm2
答:E′的大小是0.1V/m,方向竖直向下;在此情况下,经t0=0.02s时两板上有微粒击中区域的面积和是0.06π m2.
(3)解:微粒做匀速圆周运动,洛伦兹力充当向心力:m=1.0×10﹣5kg
![]()
竖直向下射出的微粒打在B板的左端恰好与B板相切,如图甲所示:d1=0.1m
当粒子源和B板右边击中点距离为直径时距离最远:如图乙所示: ![]()
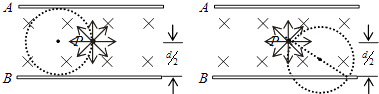
故r板被微粒打中的区域的长度都为 ![]()
答:B板被微粒打中的区域长度是 ![]() .
.
【解析】(1)微粒的初速度水平时,做类平抛运动,根据类平抛运动的规律解答.(2)要使微粒不落在金属板上,重力与电场力相平衡,微粒在水平面内做匀速直线运动.由平衡条件解答.(3)再加垂直于纸面向里的均匀磁场,重力与电场力相平衡,由洛伦兹力提供向心力做匀速圆周运动,求出微粒的轨迹半径,由几何知识即可求解.
【考点精析】通过灵活运用平抛运动,掌握特点:①具有水平方向的初速度;②只受重力作用,是加速度为重力加速度g的匀变速曲线运动;运动规律:平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动即可以解答此题.




