题目内容
12. 如图所示,足够长的光滑导轨ab、cd固定在竖直平面内,导轨间距为L,b、c两点间接一阻值为R的电阻,ef是一水平放置的导体杆,其质量为m、有效电阻值为R,杆与ab、cd保持良好接触.整个装置放在磁感应强度大小为B的匀强磁场中,磁场方向与导轨平面垂直.现用一竖直向上的力F拉导体杆,使导体杆从静止开始做加速度为$\frac{g}{2}$的匀加速直线运动,在上升高度为h的过程中,拉力做功为W,g为重力加速度,不计导轨电阻及感应电流间的相互作用.求:
如图所示,足够长的光滑导轨ab、cd固定在竖直平面内,导轨间距为L,b、c两点间接一阻值为R的电阻,ef是一水平放置的导体杆,其质量为m、有效电阻值为R,杆与ab、cd保持良好接触.整个装置放在磁感应强度大小为B的匀强磁场中,磁场方向与导轨平面垂直.现用一竖直向上的力F拉导体杆,使导体杆从静止开始做加速度为$\frac{g}{2}$的匀加速直线运动,在上升高度为h的过程中,拉力做功为W,g为重力加速度,不计导轨电阻及感应电流间的相互作用.求:(1)导体杆上升到h时所受安培力F安和拉力F;
(2)导体杆上升到h过程中通过杆的电量q;
(3)导体杆上升到h过程中bc间电阻R产生的焦耳热Q.
分析 (1)应用速度位移公式求出速度,由法拉第电磁感应定律、欧姆定律和安培力求得安培力的大小,再由牛顿第二定律求出拉力;
(2)由法拉第电磁感应定律求出电动势,由欧姆定律求出电流,由电流定义式求出电荷量;
(3)由能量守恒定律可以求出电阻产生的热量.
解答 解:(1)设ef杆上升到h时,速度为v,拉力为F,由速度位移公式得:v2-0=2ah,
解得:v=$\sqrt{2ah}$=$\sqrt{2•\frac{g}{2}•h}$=$\sqrt{gh}$
杆产生的感应电动势 E=BLv
由闭合电路欧姆定律得:I=$\frac{E}{2R}$=$\frac{BLv}{2R}$
上升到h时所受安培力 F安=BIL
联立解得 F安=$\frac{{B}^{2}{L}^{2}\sqrt{gh}}{2R}$,方向向下.
由牛顿第二定律得:F-mg-F安=ma,解得 F=$\frac{3}{2}mg$+$\frac{{B}^{2}{L}^{2}\sqrt{gh}}{2R}$.
(2)感应电量:q=$\overline{I}△t$
由闭合电路欧姆定律得:$\overline{I}$=$\frac{\overline{E}}{2R}$
由法拉第电磁感应定律得:$\overline{E}$=$\frac{△Φ}{△t}$
由以上各式得 q=$\frac{△Φ}{2R}$=$\frac{BLh}{2R}$;
(3)在整个过程中,由能量守恒定律得:W-mgh-2Q=$\frac{1}{2}$mv2-0,
电阻R上产生的热量:Q=$\frac{W}{2}$-$\frac{3mgh}{4}$;
答:
(1)导体杆上升到h时所受安培力F安大小$\frac{{B}^{2}{L}^{2}\sqrt{gh}}{2R}$,方向向下.拉力F为$\frac{3}{2}mg$+$\frac{{B}^{2}{L}^{2}\sqrt{gh}}{2R}$.
(2)导体杆上升到h过程中通过杆的电量为$\frac{BLh}{2R}$.
(3)电阻R上产生的热量为$\frac{W}{2}$-$\frac{3mgh}{4}$.
点评 电磁感应现象中的能量转化问题,分安培力做正功和做负功两种情况,本题属于安培力做负功的情况,易错的是符号.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 电场强度为零的点,电势一定为零 | |
| B. | 电场强度处处相等的区域内,电势也一定处处相等 | |
| C. | 由B=$\frac{F}{IL}$可知,B与F成正比,与IL成反比 | |
| D. | 电流在磁场中某点不受磁场力作用,则该点的磁感应强度不一定为零 |

若某一物体质量M一定时,测得a与F的有关数据如表所示.
| a/m•s-2 | 1.98 | 4.01 | 5.99 | 8.02 |
| F/N | 1.00 | 2.00 | 3.00 | 4.00 |
(2)根据图象判定:当M一定时,a与F的关系为a与F成正比.
 如图是质谱仪工作原理的示意图,带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,带电粒子的重力忽略不计.则( )
如图是质谱仪工作原理的示意图,带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,带电粒子的重力忽略不计.则( )| A. | a的质量一定大于b的质量 | |
| B. | a的电荷量一定大于b的电荷量 | |
| C. | a在磁场中运动的时间大于b运动的时间 | |
| D. | a的比荷($\frac{{q}_{a}}{{m}_{a}}$)大于b的比荷($\frac{{q}_{b}}{{m}_{b}}$) |
 如图所示,一物体静止在倾角为θ的木板上,现将倾角θ逐渐增大,物体仍然保持静止不动,则下列说法正确的是( )
如图所示,一物体静止在倾角为θ的木板上,现将倾角θ逐渐增大,物体仍然保持静止不动,则下列说法正确的是( )| A. | 物体所受的重力和摩擦力的合力在逐渐增大 | |
| B. | 物体所受的重力和支持力的合力在逐渐增大 | |
| C. | 物体所受的支持力和摩擦力的合力在逐渐增大 | |
| D. | 物体所受的重力、支持力和摩擦力的合力在逐渐增大 |

| A. | a点的电势一定低于b点的电势 | |
| B. | a点的场强一定大于b点的场强 | |
| C. | 正电荷在a点的电势能一定大于它在b点的电势能 | |
| D. | a点的场强方向一定沿着过a点的电场线向右 |

| A. | A灯变亮、B灯变亮、C灯变亮 | B. | A灯变暗、B灯变亮、C灯变暗 | ||
| C. | A灯变暗、B灯变暗、C灯变暗 | D. | A灯变亮、B灯变暗、C灯变亮 |
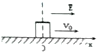 在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=4×105N/C,方向与x轴正方向相同.在O处放一个带电量q=-2×10-8 C,质量m=2克的绝缘物块.物块与水平面间的动摩擦系数μ=0.1,沿x轴正方向给物块一个初速度v0=4m/s,如图所示.求:物块最终停止在O左边的位置离O的距离.(g取10m/s2)
在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小E=4×105N/C,方向与x轴正方向相同.在O处放一个带电量q=-2×10-8 C,质量m=2克的绝缘物块.物块与水平面间的动摩擦系数μ=0.1,沿x轴正方向给物块一个初速度v0=4m/s,如图所示.求:物块最终停止在O左边的位置离O的距离.(g取10m/s2)