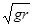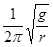题目内容
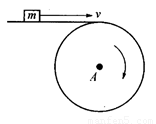
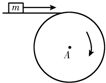 m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑.当m可被水平抛出时,
m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间、传送带与小物体间不会打滑.当m可被水平抛出时,(1)A轮每秒的转数n最少是多少?
(2)若A轮有上述的最小转速,且其最高点距地面高度为h,求小物体落地的速度方向(用反三角函数表示).
分析:(1)物体恰好不被抛出的临界条件是最高点重力恰好提供向心力,根据牛顿第二定律和向心力公式列式求解即可.
(2)物体离开传送带后做平抛运动,先根据平抛运动的分速度公式求解分速度,然后求解小物体落地的速度方向与水平方向的夹角.
(2)物体离开传送带后做平抛运动,先根据平抛运动的分速度公式求解分速度,然后求解小物体落地的速度方向与水平方向的夹角.
解答:解:(1)在轮最高点,有:
mg=
解得:v=
而:n=
=
(2)物体离开传送带后做平抛运动,有:
h=
gt2…①
vy=gt…②
tanθ=
…③
得落地速度与水平方向的夹角:
θ=arctan
答:(1)A轮每秒的转数n最少是
;
(2)小物体落地的速度方向与水平方向的夹角为arctan
.
mg=
| mv2 |
| r |
解得:v=
| gr |
而:n=
| v |
| 2πr |
| 1 |
| 2π |
|
(2)物体离开传送带后做平抛运动,有:
h=
| 1 |
| 2 |
vy=gt…②
tanθ=
| gt |
| v |
得落地速度与水平方向的夹角:
θ=arctan
|
答:(1)A轮每秒的转数n最少是
| 1 |
| 2π |
|
(2)小物体落地的速度方向与水平方向的夹角为arctan
|
点评:本题第一问关键抓住临界条件,物体恰好不被抛出的临界条件是最高点重力恰好提供向心力,然后根据牛顿第二定律列式求解;第二问关键是根据平抛运动的分运动公式列式求解.

练习册系列答案
相关题目
 (2009?江苏模拟)m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑.当m可被水平抛出时,A轮每秒的转数最少是( )
(2009?江苏模拟)m为在水平传送带上被传送的小物体(可视为质点),A为终端皮带轮,如图所示,已知皮带轮半径为r,传送带与皮带轮间不会打滑.当m可被水平抛出时,A轮每秒的转数最少是( )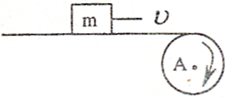 m为在水平传送带上被传送的物体,A为终端皮带轮,如图所示,半径为r,当m可被水平抛出时,A轮转速最少是:
m为在水平传送带上被传送的物体,A为终端皮带轮,如图所示,半径为r,当m可被水平抛出时,A轮转速最少是: