Question

【题目】竖直转轴上A点安装长度为L=2m的铰链（所能承受的力足够大），铰链的另一端固定质量为M=2kg的小球（视为质点），A点下方0.7m处与小球之间连接一根长度s=1.5m的轻绳，绳子能承受的最大拉力为Tm=12N。求绳子伸直时转轴转动角速度ω的取值范围？ (g＝10m/s2)

Answer 1

【答案】2.5rad/s rad/s

【解析】

设竖直杆为AB，AB杆与AM杆的夹角为，由三角形BAM中由余弦定理，因此；，；物体做匀速圆周运动的转动半径L=CM=1.2

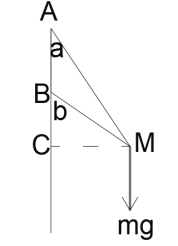
当角速度取得最小时，绳上拉力为零，由重力和杆AM的拉力提供向心力，因此有代入数据得；

随着角速度得增加，绳上得拉力逐渐增加，当绳上得拉力增加到12N时，物体得角速度达到最大，此时设绳上得拉力为T，杆上的拉力为F，因此有；

联立解得rad/s。

故角速度得取值范围2.5rad/s rad/s。