题目内容
 如图所示,用两根相同的导线绕成匝数分别为n1和n2的圆形闭合线圈A和B,两线圈平面与匀强磁场垂直.当磁感应强度随时间均匀变化时,两线圈中的感应电流之比IA:IB为( )
如图所示,用两根相同的导线绕成匝数分别为n1和n2的圆形闭合线圈A和B,两线圈平面与匀强磁场垂直.当磁感应强度随时间均匀变化时,两线圈中的感应电流之比IA:IB为( )分析:由法拉第电磁感应定律E=n
=n
πR2,求解感应电动势之比.根据电阻定律:电阻r=ρ
,感应电流I=
,联立求解感应电流之比.
| △? |
| △t |
| △B |
| △t |
| L |
| S |
| E |
| r |
解答:解:由法拉第电磁感应定律得:E=n
=n
πR2,可知,感应电动势与半径的平方成正比.
而根据电阻定律:线圈的电阻为r=ρ
=ρ
,
线圈中感应电流I=
,由上综合得到,感应电流与线圈半径成正比.即IA:IB=RA:RB;
因相同导线绕成匝数分别为n1和n2的圆形线圈,因此半径与匝数成反比,故IA:IB=n2:n1;
故选B
| △? |
| △t |
| △B |
| △t |
而根据电阻定律:线圈的电阻为r=ρ
| L |
| S |
| n?2πR |
| S |
线圈中感应电流I=
| E |
| r |
因相同导线绕成匝数分别为n1和n2的圆形线圈,因此半径与匝数成反比,故IA:IB=n2:n1;
故选B
点评:本题是法拉第电磁感应定律和电阻定律的综合应用求解感应电流之比,采用比例法研究.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
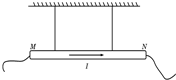 如图所示,用两根相同的轻质细绳水平悬挂一段均匀载流导体棒MN,电流I的方向从M到N,绳子的拉力均为F.为使F变大,下列说法中正确的是( )
如图所示,用两根相同的轻质细绳水平悬挂一段均匀载流导体棒MN,电流I的方向从M到N,绳子的拉力均为F.为使F变大,下列说法中正确的是( )| A、加水平向右的磁场 | B、加水平向左的磁场 | C、加垂直纸面向里的磁场 | D、加垂直纸面向外的磁场 |
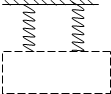 如图所示,用两根相同的轻弹簧秤吊着一根铜棒,铜棒所在的虚线范围内有垂直纸面的匀强磁场,当棒中通过向右的电流且棒静止时,弹簧处于伸长状态,弹簧秤的读数均 为F1;将棒中的电流反向,静止时弹簧秤的读数均为F2,且F2>F1.则由此可以确定 ( )
如图所示,用两根相同的轻弹簧秤吊着一根铜棒,铜棒所在的虚线范围内有垂直纸面的匀强磁场,当棒中通过向右的电流且棒静止时,弹簧处于伸长状态,弹簧秤的读数均 为F1;将棒中的电流反向,静止时弹簧秤的读数均为F2,且F2>F1.则由此可以确定 ( )| A、磁场的方向 | B、磁感应强度的大小 | C、铜棒的质量 | D、弹簧的劲度系数 |
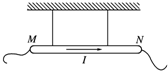 如图所示,用两根相同的细绳水平悬挂一段均匀载流直导线MN,电流I方向从M到N,绳子的拉力均为F.为使F=0,可能达到要求的方法是( )
如图所示,用两根相同的细绳水平悬挂一段均匀载流直导线MN,电流I方向从M到N,绳子的拉力均为F.为使F=0,可能达到要求的方法是( ) 如图所示,用两根相同的细绳水平悬挂一段均匀载流直导线MN,若有电流从MN上流过,绳子的拉力均为F.为使F=0,可能达到要求的方法是( )
如图所示,用两根相同的细绳水平悬挂一段均匀载流直导线MN,若有电流从MN上流过,绳子的拉力均为F.为使F=0,可能达到要求的方法是( )