题目内容
5.相距L的点电荷A、B的带电量分别为+8Q和-Q:(1)若A、B电荷固定不动,在它们连线的中点放入带电量+2Q的电荷C,电荷C受到的静电力是多少?
(2)若A、B电荷是可以自由移动的,要在通过它们的直线上引入第三个电荷D,使三个点电荷都处于平衡状态,求电荷D的电量和放置的位置.
分析 (1)根据库仑定律分别求出C受到的A的作用力和B的作用力,然后求和即可.
(2)A、B、D三个点电荷都处于静止状态,对电荷受力分析,每个电荷都处于受力平衡状态,故根据库仑定律可分别对任意两球进行分析列出平衡方程即可求得结果.
解答 解:(1)由题C到A与B的距离都是$\frac{L}{2}$,A对C的作用力:${F}_{1}=\frac{k{Q}_{A}{Q}_{C}}{(\frac{L}{2})^{2}}=\frac{k•8Q•2Q}{(\frac{L}{2})^{2}}=\frac{64k{Q}^{2}}{{L}^{2}}$;方向由A指向B;
同理C受到B的库仑力:${F}_{2}=\frac{k{Q}_{B}{Q}_{C}}{{(\frac{L}{2})}^{2}}=\frac{k•Q•2Q}{{(\frac{L}{2})}^{2}}=\frac{8k{Q}^{2}}{{L}^{2}}$方向由A指向B,
由于两个力的方向相同,所以C受到的合力:F=F1+F2=$\frac{72kQ}{{L}^{2}}$,方向由A指向B.
(2))A、B、D三个电荷要平衡,必须三个电荷的一条直线,外侧二个电荷相互排斥,中间电荷吸引外侧两个电荷;同时,由于外侧两个电荷之间距离大,要平衡中间电荷的拉力,必须外侧电荷电量大,中间电荷电量小,所以D必须为正电,在B的右侧.
设D所在位置与B的距离为r,则D所在位置与A的距离为L+r,要能处于平衡状态,
所以A对D的电场力大小等于B对D的电场力大小,设D的电量为q.则有:$\frac{k•8Qq}{(L+r)^{2}}=\frac{kQq}{{r}^{2}}$
解得:r=$\frac{2\sqrt{2}+1}{7}L$
对点电荷A,其受力也平衡,则:$\frac{k•8Qq}{{(L+r)}^{2}}=\frac{k•8Q•Q}{{L}^{2}}$
解得:q=$\frac{(2\sqrt{2}+8)}{7}Q$
答:(1)若A、B电荷固定不动,在它们连线的中点放入带电量+2Q的电荷C,电荷C受到的静电力是$\frac{72kQ}{{L}^{2}}$,方向由A指向B;
(2)使三个点电荷都处于平衡状态,电荷D的电量是$\frac{(2\sqrt{2}+8)}{7}Q$,放置的位置是B的右侧$\frac{2\sqrt{2}+1}{7}L$处.
点评 在三个电荷的平衡问题中,我们可以去尝试假设C带正电或负电,它应该放在什么地方,能不能使整个系统处于平衡状态.不行再继续判断.
也可以考虑外侧两个电荷距离大,要平衡中间电荷的拉力,必须外侧电荷电量大,中间电荷电量小,有“两大夹一小,两同夹一异”的结论.

| A. | 网球比赛中发球是至关重要的一环,罗迪克曾在戴维斯杯半决赛中发球时速达到249km/h千米,近几年尚无人超越 | |
| B. | 经提速后列车的速度达到150km/h | |
| C. | 由于堵车,在隧道内的车速仅为1.2m/s | |
| D. | 返回地面的“神舟七号”飞船以4m/s的速度落地 | |
| E. | 子弹以800m/s的速度撞击在墙上 |
 A、B是某电场中一条电场线上的两点,一正电荷仅在电场力作用下,沿电场线从A点运动到B点,速度图象如图,则( )
A、B是某电场中一条电场线上的两点,一正电荷仅在电场力作用下,沿电场线从A点运动到B点,速度图象如图,则( )| A. | EA>EB | B. | EA<EB | C. | φA<φB | D. | εA<εB |
| A. | 动能减少了$\frac{2}{3}$mgh | B. | 电势能增加了$\frac{1}{3}$mgh | ||
| C. | 重力势能减少了$\frac{2}{3}$mgh | D. | 机械能减少了$\frac{2}{3}$mgh |
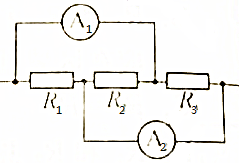 如图所示,三个电阻的阻值之比为R1:R2:R3=1:2:3,电流表的内阻忽略不计,则通过三个电阻的电流强度之比为多少?两个电流表读数之比多少?
如图所示,三个电阻的阻值之比为R1:R2:R3=1:2:3,电流表的内阻忽略不计,则通过三个电阻的电流强度之比为多少?两个电流表读数之比多少? 如图所示,水平传送带以v=2m/s的速率沿逆时针方向转动,在其左端与一竖直固定的光滑轨道平滑相接,右端与一半径R=0.4m的光滑半圆轨道相切,一质量m=2kg的物块(可视为质点)从光滑轨道上的某点由静止开始下滑,通过水平传送带后从半圆轨道的最高点水平抛出,并恰好落在传送带的最左端,已知物块通过半圆轨道最高点时受到的弹力F=60N,物块与传送带间的动摩擦因数μ=0.25,取重力加速度g=10m/s2,求:(计算结果可以保留根号)
如图所示,水平传送带以v=2m/s的速率沿逆时针方向转动,在其左端与一竖直固定的光滑轨道平滑相接,右端与一半径R=0.4m的光滑半圆轨道相切,一质量m=2kg的物块(可视为质点)从光滑轨道上的某点由静止开始下滑,通过水平传送带后从半圆轨道的最高点水平抛出,并恰好落在传送带的最左端,已知物块通过半圆轨道最高点时受到的弹力F=60N,物块与传送带间的动摩擦因数μ=0.25,取重力加速度g=10m/s2,求:(计算结果可以保留根号) (1)在用单摆测定重力加速度的实验中,下列措施中必要的或正确的做法是BCD.
(1)在用单摆测定重力加速度的实验中,下列措施中必要的或正确的做法是BCD.