题目内容
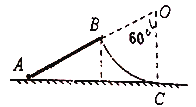
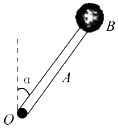
【题目】如图所示,绕同一恒星运行的两颗行星A和B,A是半径为r的圆轨道,B是长轴![]() 为2r椭圆轨道,其中Q′到恒星中心的距离为Q到恒星中心的距离的2倍,两轨道相交于P点。以下说法正确的是( )
为2r椭圆轨道,其中Q′到恒星中心的距离为Q到恒星中心的距离的2倍,两轨道相交于P点。以下说法正确的是( )

A. A和B经过P点时加速度相同
B. A和B经过P点时的速度相同
C. A和B绕恒星运动的周期相同
D. A的加速度大小与B在Q′处加速度大小之比为16:9
【答案】ACD
【解析】由牛顿第二定律得: ![]() ,解得:
,解得: ![]() ,经过P点时M、r都相同,则向心加速度相同,故A正确;A行星做匀速圆周运动,而B做的是椭圆运动,二者在同一点处的速度方向不相同,速度不同,故B错误;根据开普勒第三定律,行星和彗星围绕同一中心天体运动,且半长轴相同,故周期相同,故C正确;B在Q′处时与恒星球心的距离为
,经过P点时M、r都相同,则向心加速度相同,故A正确;A行星做匀速圆周运动,而B做的是椭圆运动,二者在同一点处的速度方向不相同,速度不同,故B错误;根据开普勒第三定律,行星和彗星围绕同一中心天体运动,且半长轴相同,故周期相同,故C正确;B在Q′处时与恒星球心的距离为![]() r,根据
r,根据![]() 故A的加速度大小与B在Q′处加速度大小之比为
故A的加速度大小与B在Q′处加速度大小之比为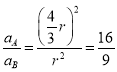 ,故D正确.故选ACD.
,故D正确.故选ACD.

练习册系列答案
相关题目