题目内容
【题目】如图所示的直角坐标系中，第一象限内分布着均匀辐射的电场，坐标原点与四分之一圆弧的荧光屏间电压为U；第三象限内分布着竖直向下的匀强电场，场强大小为E.大量电荷量为–q（q>0）、质量为m的粒子，某时刻起从第三象限不同位置连续以相同的初速度v0沿x轴正方向射入匀强电场.若粒子只能从坐标原点进入第一象限，其它粒子均被坐标轴上的物质吸收并导走而不影响原来的电场分布.不计粒子的重力及它们间的相互作用.下列说法正确的是（ ）
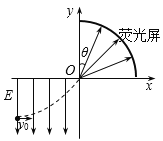
A. 能进入第一象限的粒子，在匀强电场中的初始位置分布在一条直线上
B. 到达坐标原点的粒子速度越大，入射速度方向与y轴的夹角θ越大
C. 能打到荧光屏的粒子，进入O点的动能必须大于qU
D. 若U<
，荧光屏各处均有粒子到达而被完全点亮
【答案】BCD
【解析】试题分析：带电粒子在电场中做类平抛运动，由平抛运动规律列方程求解粒子的初位置的坐标，由初位置的坐标的函数进行判断即可；（2）粒子在竖直方向做匀加速直线运动由速度时间公式求出
，根据
求正切值；（3）负电荷进入第一象限后电场力做负功，由功能关系分析到达荧光屏的粒子的特点；（4）求出粒子速度的偏转角与时间的关系，判断出粒子可以以任意夹角进入第一象限即可．
设粒子开始时的坐标为
，粒子在电场中运动过程中，由平抛运动规律及牛顿运动定律得
①，
②，
③，联立得
④，可知能进入第一象限的粒子，在匀强电场中的初始位置分布在一条抛物线上，故A错误；粒子的初速度是相等的，到达O点的粒子速度越大，则沿y方向的分速度越大．粒子到达O点时，沿+y方向的分速度
，速度与x正方向的夹角
满足： 
⑥，可知到达坐标原点的粒子速度越大，到达O点的速度方向与y轴的夹角
越大，故B正确；负电荷进入第一象限后电场力做负功，而到达荧光屏的粒子的速度必须大于等于0，由功能关系可知： 
⑦，即能打到荧光屏的粒子，进入O点的动能必须大于qU，故C正确；粒子在电场中的偏转角： 
⑧，粒子在偏转电场中运动的时间不同，则进入第一象限后速度与y轴之间的夹角不同．所以从不同的位置开始偏转的粒子，可以以任意夹角进入第一象限，所以若
，荧光屏各处均有粒子到达而被完全点亮，故D正确．
