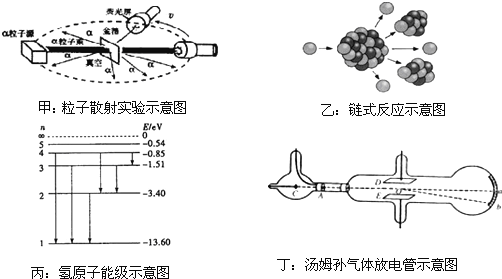
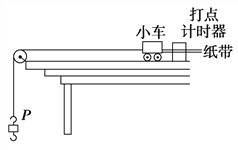
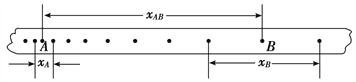
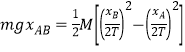题目内容
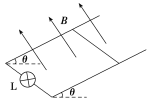
【题目】如图所示,两条相距为d=0.5 m的足够长的平行金属导轨倾斜放置,导轨与水平面间的夹角为θ=37°,导轨的下端接有阻值为R=2 Ω的小灯泡L,一质量为m=0.2 kg、电阻为r=1 Ω、长为d=0.5 m的导体棒垂直导轨放置并与导轨接触良好,导体棒和导轨间的动摩擦因数为0.5,导轨间存在垂直导轨平面向上、磁感应强度大小为B=2 T的匀强磁场.现将导体棒由静止开始释放,当导体棒沿导轨下滑的距离为x=0.46 m时,导体棒的速度达到v=0.9 m/s,且小灯泡此时正常发光,重力加速度大小g=10 m/s2,sin 37°=0.6,cos 37°=0.8,则下列说法中正确的是( )
A. 小灯泡的额定功率为0.27 W
B. 导体棒的速度达到0.9 m/s时,加速度大小为0.5 m/s2
C. 在导体棒的速度从零增大到0.9 m/s的过程中,通过小灯泡L的电荷量约为0.15 C
D. 在导体棒的速度从零增大到0.9 m/s的过程中,小灯泡L上产生的热量约为0.069 J
【答案】BCD
【解析】
A、当导体棒的速度为v=0.9 m/s时,小灯泡正常发光,小灯泡的额定功率为PL=I2R,而I=![]() ,E=Bdv,代入数据可得PL=0.18 W,选项A错误;
,E=Bdv,代入数据可得PL=0.18 W,选项A错误;
B、当导体棒的速度达到v=0.9 m/s时,对导体棒由牛顿第二定律有mgsin θ-μmgcos θ-![]() =ma,代入数据解得a=0.5 m/s2,选项B正确;
=ma,代入数据解得a=0.5 m/s2,选项B正确;
C、导体棒的速度从零增大到0.9 m/s的过程中,导体棒沿导轨下滑了x=0.46 m,故q=![]() Δt=
Δt=![]() ≈0.15 C,选项C正确;
≈0.15 C,选项C正确;
D、导体棒的速度从零增大到0.9 m/s的过程中,小灯泡上产生的热量为QL,由能量守恒定律可得QL=![]() (mgxsin θ-μmgxcos θ-
(mgxsin θ-μmgxcos θ-![]() mv2)=0.069 J,选项D正确。
mv2)=0.069 J,选项D正确。