题目内容
 (2010?威海二模)如图甲所示,在以O为坐标原点的xoy平面内,存在着范围足够大的电场和磁场.一个质量m=2×10-2kg,带电量q=+5×10-3C的带电小球在0时刻以v0=40m/s的速度从O点沿+x方向(水平向右)射入该空间,在该空间同时加上如图乙所示的电场和磁场,其中电场沿-y方向(竖直向上),场强大小E0=40V/m.磁场垂直于xoy平面向外,磁感应强度大小B0=4πT.取当地的重力加速度g=10m/s2,不计空气阻力,计算结果中可以保留根式或π.试求:
(2010?威海二模)如图甲所示,在以O为坐标原点的xoy平面内,存在着范围足够大的电场和磁场.一个质量m=2×10-2kg,带电量q=+5×10-3C的带电小球在0时刻以v0=40m/s的速度从O点沿+x方向(水平向右)射入该空间,在该空间同时加上如图乙所示的电场和磁场,其中电场沿-y方向(竖直向上),场强大小E0=40V/m.磁场垂直于xoy平面向外,磁感应强度大小B0=4πT.取当地的重力加速度g=10m/s2,不计空气阻力,计算结果中可以保留根式或π.试求:(1)12s末小球速度的大小.
(2)在给定的xoy坐标系中,大体画出小球在0~24s内运动轨迹的示意图.
(3)26s末小球的位置坐标.
分析:(1)正确对小球进行受力分析,明确运动形式,求出圆周运动的周期和所给时间直间的关系,最后利用平抛运动规律求解;
(2)根据第一问的解答,可正确画出图象;
(3)利用运动的周期性画出26s内小球运动轨迹图,然后利用数学知识求解.
(2)根据第一问的解答,可正确画出图象;
(3)利用运动的周期性画出26s内小球运动轨迹图,然后利用数学知识求解.
解答:解:(1)0~1s内,小球只受重力作用,做平抛运动.当同时加上电场和磁场时,电场力:F1=qE0=0.2N,方向向上,
重力:G=mg=0.2N,方向向下,重力和电场力恰好平衡.此时小球只受洛伦兹力而做匀速圆周运动,
根据牛顿第二定律有:qvB0=
运动周期T=
,联立解得T=2s
正好是电场、磁场同时存在时间的5倍,即在这10s内,小球恰好做了5个完整的匀速圆周运动.所以小球在t1=12s时刻的速度相当于小球做平抛运动t=2s时的末速度.
vy=gt=20m/s,
vx=v0=40m/s
v1=
=20
m/s
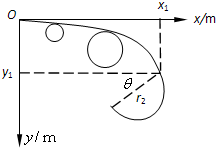 (2)小球在24s内的运动轨迹示意图如图所示
(2)小球在24s内的运动轨迹示意图如图所示
(3)分析可知,小球26s末与24s末的位置相同,在26s内小球做了3s的平抛运动,23s末小球平抛运动的位移大小为:
x1=v0?3=120m
y1=
g×32=45m
3s时小球的速度大小为v2=
=50m/s
速度与竖直方向的夹角为θ=53°
此后小球做匀速圆周运动的半径r2=
=
m
26s末,小球恰好完成了半个圆周运动,此时小球的位置坐标
x2=x1-2r2cosθ=(120-
)m
y2=y1+2r2sinθ=(45+
)m
答:(1)12s末小球速度的大小20
m/s.
(2)0~24s内运动轨迹的如图.
(3)26s末小球的位置坐标[(120-
)m,(45+
)m].
重力:G=mg=0.2N,方向向下,重力和电场力恰好平衡.此时小球只受洛伦兹力而做匀速圆周运动,
根据牛顿第二定律有:qvB0=
| mv2 |
| r |
运动周期T=
| 2πr |
| v |
正好是电场、磁场同时存在时间的5倍,即在这10s内,小球恰好做了5个完整的匀速圆周运动.所以小球在t1=12s时刻的速度相当于小球做平抛运动t=2s时的末速度.
vy=gt=20m/s,
vx=v0=40m/s
v1=
|
| 5 |
 (2)小球在24s内的运动轨迹示意图如图所示
(2)小球在24s内的运动轨迹示意图如图所示(3)分析可知,小球26s末与24s末的位置相同,在26s内小球做了3s的平抛运动,23s末小球平抛运动的位移大小为:
x1=v0?3=120m
y1=
| 1 |
| 2 |
3s时小球的速度大小为v2=
|
速度与竖直方向的夹角为θ=53°
此后小球做匀速圆周运动的半径r2=
| mv2 |
| qB0 |
| 50 |
| π |
26s末,小球恰好完成了半个圆周运动,此时小球的位置坐标
x2=x1-2r2cosθ=(120-
| 60 |
| π |
y2=y1+2r2sinθ=(45+
| 80 |
| π |
答:(1)12s末小球速度的大小20
| 5 |
(2)0~24s内运动轨迹的如图.
(3)26s末小球的位置坐标[(120-
| 60 |
| π |
| 80 |
| π |
点评:解答带电粒子在磁场中运动的思路是正确受力分析,画出运动轨迹图,这类问题对学生数学知识要求较高,是考查重点和难点.

练习册系列答案
相关题目
 (2010?威海二模)如图甲所示,A、B两长方体叠放在一起,放在光滑的水平面上,物体B从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止.则在0~2t0时间内,下列说法正确的是( )
(2010?威海二模)如图甲所示,A、B两长方体叠放在一起,放在光滑的水平面上,物体B从静止开始受到一个水平变力的作用,该力与时间的关系如图乙所示,运动过程中A、B始终保持相对静止.则在0~2t0时间内,下列说法正确的是( ) (2010?威海二模)如图所示,平放在水平面上的轻质弹簧的一端固定在竖直墙上,质量为m1的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接.一个质量为m2的小球从槽高处由静止开始下滑,要使小球能与弧形槽发生第二次作用,m1、m2应满足怎样的条件?
(2010?威海二模)如图所示,平放在水平面上的轻质弹簧的一端固定在竖直墙上,质量为m1的光滑弧形槽静止在光滑水平面上,底部与水平面平滑连接.一个质量为m2的小球从槽高处由静止开始下滑,要使小球能与弧形槽发生第二次作用,m1、m2应满足怎样的条件? (2010?威海二模)如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有一质量为m、阻值为R的闭合矩形金属线框abcd,用绝缘轻质细杆悬挂在O点,并可绕O点无摩擦摆动.金属线框从右侧某一位置由静止开始释放,细杆和金属框平面始终处于垂直纸面的同一平面内,不计空气阻力.下列判断正确的是( )
(2010?威海二模)如图所示,在磁感应强度大小为B、方向竖直向上的匀强磁场中,有一质量为m、阻值为R的闭合矩形金属线框abcd,用绝缘轻质细杆悬挂在O点,并可绕O点无摩擦摆动.金属线框从右侧某一位置由静止开始释放,细杆和金属框平面始终处于垂直纸面的同一平面内,不计空气阻力.下列判断正确的是( ) (2010?威海二模)如图所示,为一自耦变压器的电路图,其特点是铁芯上只绕有一个线圈.把整个线圈作为原线圈,而取线圈的一部分作为副线圈.原线圈接在电压恒为U的正弦交流电源上,电流表Al、A2均为理想电表.当触头P向上移动时,下列说法正确的是( )
(2010?威海二模)如图所示,为一自耦变压器的电路图,其特点是铁芯上只绕有一个线圈.把整个线圈作为原线圈,而取线圈的一部分作为副线圈.原线圈接在电压恒为U的正弦交流电源上,电流表Al、A2均为理想电表.当触头P向上移动时,下列说法正确的是( )