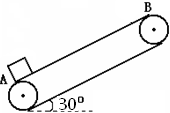
题目内容
 传送带与地面成夹角θ=37°,以11m/s 的速度逆时针转动,有一物块在传送带右上方以v0=4m/s的速度水平抛出,恰好无碰撞落入传送带上端A位置处,它与传送带间的动摩擦因数μ=0.75,已知传送带从A到B的长度L=16m,物块质量1kg,则
传送带与地面成夹角θ=37°,以11m/s 的速度逆时针转动,有一物块在传送带右上方以v0=4m/s的速度水平抛出,恰好无碰撞落入传送带上端A位置处,它与传送带间的动摩擦因数μ=0.75,已知传送带从A到B的长度L=16m,物块质量1kg,则(1)物体从A到B需要的时间为多少;
(2)从A到B摩擦力做多少功;
(3)从A到B摩擦生热是多少.
分析:(1)由平抛运动的规律可知物块的速度;由牛顿第二定律明确其加速度,假设其在传送带上达最大速度,则由运动学公式可求其位移,判断是否已离开传送带;经判断物块达最大速度时仍在传送带上,再由匀速直线运动规律可求得匀速过程的时间;即可求得总时间;
(2)加速过程为滑动摩擦力做功,匀速过程为静摩擦力做功,由功的公式可求得总功;
(3)摩擦生热等于摩擦力与相对位移间的乘积.
(2)加速过程为滑动摩擦力做功,匀速过程为静摩擦力做功,由功的公式可求得总功;
(3)摩擦生热等于摩擦力与相对位移间的乘积.
解答:解:由平抛运动规律可知:
VA=
=5m/s;
由牛顿第二定律可知:
a=
=12m/s2;
加速度只能维持到物体的速度达到11m/s为止,其对应的时间和位移分别为:
t1=
=0.5s;
s1=
=4m<16m;
因mgsinθ=μmgcosθ,故以后物体受到的摩擦力变为沿传送带向上,其加速度大小为零,设物体完成剩余的位移s2所用时间为t2;
则s2=v传t2,16m-4m=11t2;
解得t2=1.2s,所以:t总=0.5+1.1s=1.6s;
(2)滑动摩擦力做功Wf=-μmgcos37°s1-mgsin37°s2=-48J;
(3)在t1时间内传送带位移s传=v传t1
在t1时间内物体块与传送带发生相对滑动,s相=s传-s1=1.5m;
故摩擦生热Q=μmgcos37°s相=9J;
答:(1)总时间为1.6s;(2)摩擦力做功为-48J;(3)产生的热量为9J.
VA=
| v0 |
| cos37° |
由牛顿第二定律可知:
a=
| mgsin37°+μmgcos37° |
| m |
加速度只能维持到物体的速度达到11m/s为止,其对应的时间和位移分别为:
t1=
| v传-vA |
| a |
s1=
| ||||
| 2a |
因mgsinθ=μmgcosθ,故以后物体受到的摩擦力变为沿传送带向上,其加速度大小为零,设物体完成剩余的位移s2所用时间为t2;
则s2=v传t2,16m-4m=11t2;
解得t2=1.2s,所以:t总=0.5+1.1s=1.6s;
(2)滑动摩擦力做功Wf=-μmgcos37°s1-mgsin37°s2=-48J;
(3)在t1时间内传送带位移s传=v传t1
在t1时间内物体块与传送带发生相对滑动,s相=s传-s1=1.5m;
故摩擦生热Q=μmgcos37°s相=9J;
答:(1)总时间为1.6s;(2)摩擦力做功为-48J;(3)产生的热量为9J.
点评:本题用传送带综合考查了平抛、功能关系、牛顿运动定律等内容;对学生的要求较高;应注意正确判断物体的运动过程,再选择相应的规律求解.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图所示,传送带与地面成夹角θ=37°,以10m/s的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.9,已知传送带从A→B的长度L=50m,则物体从A到B需要的时间为多少?
如图所示,传送带与地面成夹角θ=37°,以10m/s的速度顺时针转动,在传送带下端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.9,已知传送带从A→B的长度L=50m,则物体从A到B需要的时间为多少?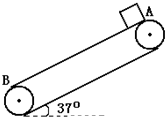 如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带从A→B的长度L=16m,则物体从A到B需要的时间为多少?
如图所示,传送带与地面成夹角θ=37°,以10m/s的速度逆时针转动,在传送带上端轻轻地放一个质量m=0.5㎏的物体,它与传送带间的动摩擦因数μ=0.5,已知传送带从A→B的长度L=16m,则物体从A到B需要的时间为多少?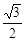 ,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,
,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,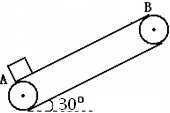
 ,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,
,已知传送带从A到传送带顶端B的长度L=15m,物体从A运动到B的过程中,