题目内容
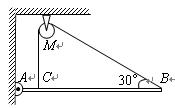
如图，OA是一根长为L=0.3m的轻质硬杆，其一端通过光滑铰链与竖直光滑墙面连接，另一端A固定一质量均匀分布的球B，O′点为球心，O、A、O′三点在一条直线上，B球半径为r=0.2m，质量为M=3.0kg．矩形物块C的厚度为d=0.1m，质量为m=2.0kg，物块与球面间的动摩擦因数为μ=0.4．现在物块下端施加一个竖直向上、大小为30N的力F，使物块保持静止．g=10m/s2．求：
（1）B球对物块C的摩擦力和压力的大小；
（2）撤去力F后，B球对物块C的摩擦力大小．
（1）B球对物块C的摩擦力和压力的大小；
（2）撤去力F后，B球对物块C的摩擦力大小．
（1）对于物块C：Ff=F-mg=10N，方向竖直向下．
B球处于力矩平衡状态：Mf+MN=MG
即Ffd+N
=Mg(d+r)
代入解得FN=20N
根据牛顿第三定律，B对C的压力大小为20N，方向水平向左．
（2）撤去力F后，物块C将向下滑动，C对球B的摩擦力方向向下，
此时B球仍处于力矩平衡状态：Mf′+MG=MN′
即μN′d+Mg(d+r)=N′
代入解得FN′=25N，Ff=μN′=10N
故B球对物块C的摩擦力大小为10N．
答：（1）B球对物块C的摩擦力为10N，压力的大小为20N；
（2）撤去力F后，B球对物块C的摩擦力大小为10N．
B球处于力矩平衡状态：Mf+MN=MG
即Ffd+N
| (L+r)2-(d+r)2 |
代入解得FN=20N
根据牛顿第三定律，B对C的压力大小为20N，方向水平向左．
（2）撤去力F后，物块C将向下滑动，C对球B的摩擦力方向向下，
此时B球仍处于力矩平衡状态：Mf′+MG=MN′
即μN′d+Mg(d+r)=N′
| (L+r)2-(d+r)2 |
代入解得FN′=25N，Ff=μN′=10N
故B球对物块C的摩擦力大小为10N．
答：（1）B球对物块C的摩擦力为10N，压力的大小为20N；
（2）撤去力F后，B球对物块C的摩擦力大小为10N．
练习册系列答案
相关题目
、
、
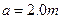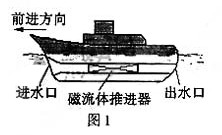
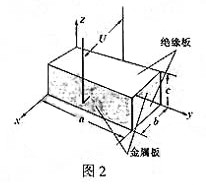
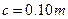。工作时，在通道内沿z轴正方向加
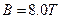的匀强磁场；沿x轴负方向加匀强电场，使两金属板间的电压
；海水沿y轴方向流过通道。已知海水的电阻率
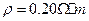
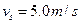的速度匀速前进。若以船为参照物，海水以
的速率涌入进水口，由于通道的截面积小于进水口的截面积，在通道内海水速率增加到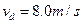
。求此时两金属板间的感应电动势U感；
U感计算，海水受到电磁力的80%可以转化为对船的推力。当船以
