题目内容
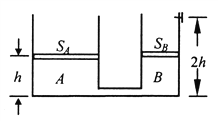
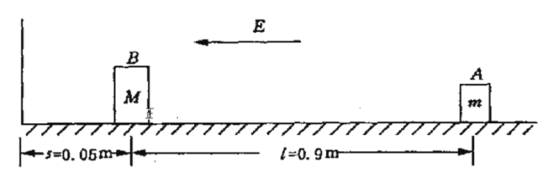
【题目】如图所示,在动摩擦因数为μ=0.50 的绝缘水平面上放置一质量为m=2.0×10-3kg的带正电的小滑块 A,所带电荷量为q=1.0×10-7C.在 A 的左边 l=0.9m 处放置一个质量M=6.0×10-3kg的不带电的小滑块 B,滑块 B 与左边竖直绝缘墙壁相距 s=0.05m,在水平面上方空间加一方向水平向左的匀强电场,电场强度为E= 4.0×105N/C.A 由静止开始向左滑动并与 B 发生碰撞,设碰撞过程的时间极短,碰撞后两滑块结合在一起共同运动并与墙壁相碰撞,在与墙壁碰撞时没有机械能损失,也没有电量的损失,且两滑块始终没有分开, 两滑块的体积大小可忽略不计.(g取10N/kg)
(1)试通过计算分析 A 和 B 的运动情况.
(2)两滑块在粗糙水平面上运动的整个过程中,由于摩擦而产生的热量是多少?(结果保留两位有效数字)
【答案】(1)A、B与墙壁碰后一起向右做匀减速直线运动,直至速度减为零,之后,两物体保持静止状态(2)1.4×10-2J
【解析】
(1)滑块A受电场qE=4.0×10-2N,方向向左,摩擦力f=μmg=1.0×10-2N,方向向右.在这两个力作用下向左做初速度为零的匀加速直线运动,直到与B发生碰撞.
滑块A与B碰撞并结合在一起后,电场的大小仍为qE=4.0×10-2N,方向向左,摩擦力的大小为f=μ(m+M)g=4.0×10-2N,方向向右.A、B所受合力为零,所以A、B碰后一起向着墙壁做匀速直线运动.
A、B一起与墙壁撞后,两滑块受到的电场力与摩擦力的大小不变,方向都是向左的,所以A、B与墙壁碰后一起向右做匀减速直线运动,直至速度减为零,之后,两物体保持静止状态.
(2)在A、B碰撞之前摩擦力做功为:
W1=μmgl=9.0×10-3J
A、B碰撞前的过程,由动能定理,得:
![]()
![]()
根据动量守恒定律,得两滑块碰后运动的速度大小为:
![]()
两滑块共同运动,与墙壁发生碰撞后返回直到静止,这段过程中,设两滑块最后静止的位置距墙壁的距离为L2,根据动能定理,
![]()
在A、B碰撞之后到两滑块停下的过程中,滑块克服摩擦力做功为
![]()
整个过程中和生的热Q等于滑块克服摩擦力做功的总和,即
![]()