题目内容
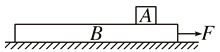
【题目】如图所示，规定水平向右为正方向，一质点从A点静止出发，以加速度a（a＞0）做匀加速直线运动到B点，接着以加速度﹣a做匀变速运动，然后返回通过A点继续向左运动，已知AB距离为S，求：
（1）质点第一次通过B点时的速度VB；
（2）质点回到A点前，离A点的最大距离x；
（3）质点从出发到再次回到A点所需要的时间t．
【答案】
（1）解：质点从A﹣B过程：
由v2﹣0=2as得，质点第一次通过B点时的速度：
vB= 
．
答：质点第一次通过B点时的速度vB= ；
（2）解：由对称性可知，由B点到减速到零，位移与A﹣B的位移相同，也等于s：
质点回到A点前，离A点的最大距离x=2s，
答：质点回到A点前，离A点的最大距离x=2s；
（3）解：由s= 
at2得，质点从A﹣B过程所用的时间：
t1= 
，
由（2）可知，质点从B到速度减小为零的过程所用的时间t1′=t1= ，
质点反向运动过程中的位移大小x=2s，
由x= at2得，质点反向运动过程所用的时间：
t2= 
= 
=2 
，
则质点从出发到再次回到A点所需要的时间：
t=t1+t1′+t2=2 +2 =2 （ 
+1）．
答：质点从出发到再次回到A点所需要的时间t=2 （ +1）．
【解析】（1）根据匀变速直线运动位移与速度的关系v2﹣0=2as即可求出质点第一次通过B点时的速度；（2）根据对称性可知由B点到减速到零的位移与A﹣B的位移相同，进而得出质点回到A点前离A点的最大距离；（3）根据s= at2求出质点从A﹣B过程所用的时间，从而知道质点从B到速度减小为零的过程所用的时间，
再利用位移时间公式求出质点反向运动过程所用的时间，三者相加即可求出质点从出发到再次回到A点所需要的时间．
【考点精析】根据题目的已知条件，利用匀变速运动中的平均速度的相关知识可以得到问题的答案，需要掌握平均速度：V=V0+Vt．
