题目内容
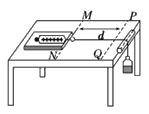
【题目】宇宙中两颗靠得比较近的恒星,只受到彼此之间的万有引力互相绕转,称之为双星系统,在浩瀚的银河系中,多数恒星都是双星系统,设某双星系统A、B绕其连线上的O点做匀速圆周运动,如图所示。若AO>OB,则( )
![]()
A. 星球A的质量一定小于B的质量
B. 星球A的角速度一定大于B的角速度
C. 双星间距离一定,双星的总质量越大,其转动周期越大
D. 双星的质量一定,双星之间的距离越大,其转动周期越大
【答案】AD
【解析】双星系统中两颗恒星间距不变,是同轴转动,角速度相等,周期也相等,故B C错误;双星靠相互间的万有引力提供向心力,所以向心力相等,故:mArAω2=mBrBω2,因为rB<rA,所以mB>mA,即B的质量一定大于A的质量,故A正确;根据牛顿第二定律,有:![]() ,其中:rA+rB=L,联立解得:T=2π
,其中:rA+rB=L,联立解得:T=2π![]() ,故双星的质量一定时,双星之间的距离L越大,其转动周期越大,故D正确;故选AD。
,故双星的质量一定时,双星之间的距离L越大,其转动周期越大,故D正确;故选AD。

【题目】某同学利用如图所示的装置验证动能定理。固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺放好木板、白纸、复写纸。将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x。改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:
高度 H(h为单位长度) | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
水平位移 x/cm | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |

(1)已知斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ,斜槽底端离地的高度为y,不计小球与水平槽之间的摩擦,小球从斜槽上滑下的过程中,动能定理若成立应满足的关系式是____________________;
(2)以H为横坐标,以__________为纵坐标,在坐标纸上描点作图,如图乙所示;

(3)由第(1)、(2)问,可以得出结论:_____________________________________________