题目内容
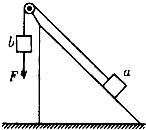如图所示，足够长粗糙斜面固定在水平面上，物块a通过平行于斜面的轻绳跨过光滑轻滑轮与物块b相连，b的质量为m．开始时，a、b均静止且a刚好不受斜面摩擦力作用．现对b施加竖直向下的恒力F，使a、b做加速运动，则在b下降h高度过程中（ ）A、a的加速度为
| ||
| B、a的重力势能增加mgh | ||
| C、绳的拉力对a做的功等于a机械能的增加 | ||
| D、F对b做的功与摩擦力对a做的功之和等于a、b动能的增加 |
分析：通过开始时，a、b及传送带均静止且a不受传送带摩擦力作用，根据共点力平衡得出a、b的质量关系．根据b上升的高度得出a下降的高度，从而求出a重力势能的减小量，根据能量守恒定律判断摩擦力功与a、b动能以及机械能的关系．
解答：解：A、开始时，a、b及传送带均静止且a不受传送带摩擦力作用，有magsinθ=mbg，则ma=
．
a的加速度与B的加速度相等，对b，根据牛顿第二定律：F-T=ma，而T＞0，故a＜
，A错误；
B、b下降h，则a上升hsinθ，则a重力势能的增加量为mag×hsinθ=mgh．故B正确．
C、根据能量守恒得，系统机械能增加，摩擦力对a做的功等于a、b机械能的增量．所以摩擦力做功大于a的机械能增加．因为系统重力势能不变，所以摩擦力做功等于系统动能的增加．故C错误．
D、对系统，合外力做的功等于动能的增加，即F对b做的功与摩擦力对a做的功与重力对a和b做的功之和，而重力对b做负功，对a做正功，且绝对值相等，故重力对系统做功之和为0，则F对b做的功与摩擦力对a做的功之和等于动能增加．故D正确．
故选：BD．
| m |
| sinθ |
a的加速度与B的加速度相等，对b，根据牛顿第二定律：F-T=ma，而T＞0，故a＜
| F |
| m |
B、b下降h，则a上升hsinθ，则a重力势能的增加量为mag×hsinθ=mgh．故B正确．
C、根据能量守恒得，系统机械能增加，摩擦力对a做的功等于a、b机械能的增量．所以摩擦力做功大于a的机械能增加．因为系统重力势能不变，所以摩擦力做功等于系统动能的增加．故C错误．
D、对系统，合外力做的功等于动能的增加，即F对b做的功与摩擦力对a做的功与重力对a和b做的功之和，而重力对b做负功，对a做正功，且绝对值相等，故重力对系统做功之和为0，则F对b做的功与摩擦力对a做的功之和等于动能增加．故D正确．
故选：BD．
点评：本题是力与能的综合题，关键对初始位置和末位置正确地受力分析，以及合力选择研究的过程和研究的对象，运用能量守恒进行分析．
练习册系列答案
阅读快车系列答案
相关题目
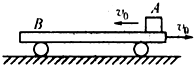如图所示，足够长的小平板车B的质量为M，以水平速度υ0向右在光滑水平面上运动，与此同时，质量为m的小物体A从车的右端以水平速度υ0沿车的粗糙上表面向左运动．若物体与车面之间的动摩擦因数为μ，则在足够长的时间内（ ）
（2011?湛江模拟）如图所示，足够长的水平粗糙轨道与固定在水平面上的光滑弧形轨道在P点相切，质量为m的滑块B静止于P点；质量为2m的滑块A由静止开始沿着光滑弧形轨道下滑，下滑的起始位置距水平轨道的高度为h，滑块A在P点与静止的滑块B碰撞后，两滑块粘合在一起共同向左运动．两滑块均可视为质点，且与水平轨道的动摩擦因素均为μ，P点切线水平．求：
如图所示，足够长的木板B放在粗糙的水平面上，木块A放在B的上面，A的右端通过一不可伸长的轻绳固定在竖直墙上，用水平恒力F向左拉动B，使其以速度v做匀速运动，此时轻绳水平且拉力大小为T，下面说法正确的是（ ）
如图所示，足够长的水平传送带AB以v1的速度匀速向右运动，另有一物体从传送带的右端向左以v2的速度滑上传送带，水平面光滑，传送带表面粗糙，以下说法正确的是（ ）