题目内容
5.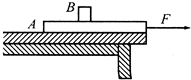 如图所示,平板A长L=5m,质量M=5kg,放在水平桌面上,板右端与桌边相齐.在 A 上距右端 s=3m处放一物体B(大小可忽略),其质量m=2kg,已知A、B 间动摩擦因数 μ 1=0.1,A与桌面间和B与桌面间的动摩擦因数μ 2=0.2,原来系统静止.现在在板的右端施一大小恒定的水平力F持续作用在物体A上直到将A从B下抽出才撤去,且使B最后停于桌的右边缘,取g=10m/s2,求:
如图所示,平板A长L=5m,质量M=5kg,放在水平桌面上,板右端与桌边相齐.在 A 上距右端 s=3m处放一物体B(大小可忽略),其质量m=2kg,已知A、B 间动摩擦因数 μ 1=0.1,A与桌面间和B与桌面间的动摩擦因数μ 2=0.2,原来系统静止.现在在板的右端施一大小恒定的水平力F持续作用在物体A上直到将A从B下抽出才撤去,且使B最后停于桌的右边缘,取g=10m/s2,求:(1)力F满足何条件可将A从B下抽出?
(2)力F的大小为多少?
分析 (1)要使A能从B下抽出,则A的加速度要大于B的加速度,根据牛顿第二定律求出物体B与A发生相对滑动时的加速度以及A的加速度,根据A的加速度要大于B的加速度求解即可;
(2)根据牛顿第二定律求出物体B与A发生相对滑动时的加速度,再对A运用牛顿第二定律,结合运动学公式求出将A从B下抽出,且恰使B停在桌右边缘拉力F的大小.
解答 解:(1)要使A能从B下抽出,则A的加速度要大于B的加速度,设拉力大小为F,根据牛顿第二定律得:
B的加速度为:${a}_{B}=\frac{{μ}_{1}mg}{m}{=μ}_{1}g=1m/{s}^{2}$,
A的加速度为:${a}_{A}=\frac{F-{μ}_{2}(M+m)g{-μ}_{1}mg}{M}$=$\frac{F-16}{5}$,
当$\frac{F-16}{5}>1$时,可将A从B下抽出,解得:F>21N
(2)B脱离A后B的加速度大小为:${a}_{B}′{=μ}_{2}g=2m/{s}^{2}$
根据匀变速直线运动的公式有:
a1t1-a2t2=0…①
$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}+\frac{1}{2}{a}_{2}{{t}_{2}}^{2}=3m$…②
联立①②解得?:t1=2s,t2=1s.
根据$\frac{1}{2}{a}_{A}{t}^{2}-\frac{1}{2}{a}_{B}{t}^{2}=2m$,t=t1=2s得:${a}_{A}=2m/{s}^{2}$.
根据牛顿第二定律得:${a}_{A}=\frac{F-{μ}_{2}(M+m)g{-μ}_{1}mg}{M}$,
解得:F=26N.
答:(1)力F满足F>21N时可将A从B下抽出;
(2)F的大小为26N.
点评 解决本题的关键能够正确地进行受力分析,结合牛顿第二定律和运动学公式进行求解,注意位移关系在解题中的应用.

 海豚喜欢在海面跳跃,如图所示是某海豚从海水里加速,再跃出水面,然后落回水面的v-t图象,下列对图象的解读正确的是( )
海豚喜欢在海面跳跃,如图所示是某海豚从海水里加速,再跃出水面,然后落回水面的v-t图象,下列对图象的解读正确的是( )| A. | 前3s海豚在水里 | B. | 2~4s内海豚在空中 | ||
| C. | 0~2s内水对海豚的作用力逐渐减小 | D. | 海豚在水里的加速距离为10m |
 如图所示,斜面上量物块A、B的质量均为m,A、B间用一个细线相连,A、B与斜面间的动摩擦因数分别为μ1,μ2,斜面倾角为θ=37°,它们以a=2m/s2一起匀加速下滑(g=10m/s2),下列说法正确的是( )
如图所示,斜面上量物块A、B的质量均为m,A、B间用一个细线相连,A、B与斜面间的动摩擦因数分别为μ1,μ2,斜面倾角为θ=37°,它们以a=2m/s2一起匀加速下滑(g=10m/s2),下列说法正确的是( )| A. | 物块B一定受4个力 | B. | μ1≥μ2 | ||
| C. | μ1≤0.5 | D. | μ2≤0.5 |
 如图电路所示,R1:R2:$R_3^{\;}$=1:2:3当ab两端接入60V电压时,cd段端输出电压等于( )
如图电路所示,R1:R2:$R_3^{\;}$=1:2:3当ab两端接入60V电压时,cd段端输出电压等于( )| A. | 60V | B. | 30V | C. | 15V | D. | 10V |
 如图所示,在一条直线上有两个相距0.4m的点电荷A、B.A带电荷量+Q,B带电-9Q.现引入第三个点电荷C,恰好使第三个点电荷C处于平衡状态,问:
如图所示,在一条直线上有两个相距0.4m的点电荷A、B.A带电荷量+Q,B带电-9Q.现引入第三个点电荷C,恰好使第三个点电荷C处于平衡状态,问: 如图所示,倾角为30°的光滑斜面AB长为0.8m,质量为1kg的物块在沿斜面向上的恒力F作用下从斜面底端由静止开始运动,当物块沿斜面运动0.2m时撤去外力,此后物块恰能滑行到B点,取g=10m/s2,求:
如图所示,倾角为30°的光滑斜面AB长为0.8m,质量为1kg的物块在沿斜面向上的恒力F作用下从斜面底端由静止开始运动,当物块沿斜面运动0.2m时撤去外力,此后物块恰能滑行到B点,取g=10m/s2,求: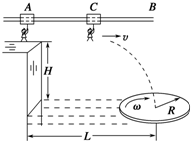 某电视台“快乐向前冲”节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
某电视台“快乐向前冲”节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R,角速度为ω,铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零,加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.