题目内容
计划发射一颗距离地面高度为地球半径R0的圆形轨道地球卫星，卫星轨道平面与赤道平面重合，已知地球表面重力加速度为g，
（1）求出卫星绕地心运动周期T
（2）设地球自转周期T0，该卫星绕地旋转方向与地球自转方向相同，则在赤道上某一点的人能连续看到该卫星的时间是多少？
（1）求出卫星绕地心运动周期T
（2）设地球自转周期T0，该卫星绕地旋转方向与地球自转方向相同，则在赤道上某一点的人能连续看到该卫星的时间是多少？
分析：（1）要求卫星绕地球运动的周期，可利用万有引力提供卫星做圆周运动的向心力即
=m
（2R0）求解T，要求T必须知道地球的质量M，而由于地球的质量未知，但地球表面的重力加速度g已知，故应该利用黄金代换公式
=mg求出地球的质量M．
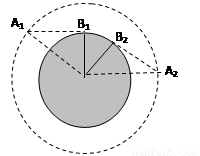
（2）当卫星与观察者的连线与观察者所在的地球的半径垂直时观察者开始看到卫星，当卫星与人的连线与人所在的地球的半径垂直时人对卫星的观察结束，故人随地球转动时人转过的圆心角为OB1与OB2的夹角，该夹角大小为
2π，卫星也在绕地球运动，其转过的角度为
2π，而OA2与OB2之间的夹角等于OA1与OB1之间的夹角设为θ，而则cosθ=
=
，故θ=
．所以
+
2π=
2π．
| GMm |
| (2R0)2 |
| 4π2 |
| T2 |
| GMm |
| R02 |
（2）当卫星与观察者的连线与观察者所在的地球的半径垂直时观察者开始看到卫星，当卫星与人的连线与人所在的地球的半径垂直时人对卫星的观察结束，故人随地球转动时人转过的圆心角为OB1与OB2的夹角，该夹角大小为
| t |
| T0 |
| t |
| T |
| OB1 |
| OA1 |
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| t |
| T0 |
| t |
| T |
解答：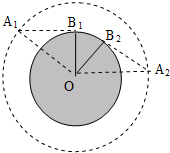
解：（1）地球对卫星的引力提供卫星做匀速圆周运动的向心力，故有
=m
（2R0）
由于地球的质量未知，而地球表面的重力加速度g已知，
故有
=mg
联立以上二式可得卫星绕地心运动周期T=2π
=4π
（2）设人在B1位置刚好看见卫星出现在A1位置，最后在B2位置看到卫星从A2位置消失，OA1=2OB1
设∠A1OB1=∠A2OB2=θ
则cosθ=
=
，
所以θ=
设人从B1位置到B2位置的时间为t，则人转过的角度为
2π，
卫星转过的角度为
2π，
故有
+
2π=
2π，
将卫星绕地心运动周期T=2π
代入上式可得
t=
=
=
答：（1）卫星绕地心运动周期T等于4π
．
（2）在赤道上某一点的人能连续看到该卫星的时间是
．
解：（1）地球对卫星的引力提供卫星做匀速圆周运动的向心力，故有| GMm |
| (2R0)2 |
| 4π2 |
| T2 |
由于地球的质量未知，而地球表面的重力加速度g已知，
故有
| GMm |
| R02 |
联立以上二式可得卫星绕地心运动周期T=2π
|
|
（2）设人在B1位置刚好看见卫星出现在A1位置，最后在B2位置看到卫星从A2位置消失，OA1=2OB1
设∠A1OB1=∠A2OB2=θ
则cosθ=
| OB1 |
| OA1 |
| 1 |
| 2 |
所以θ=
| π |
| 3 |
设人从B1位置到B2位置的时间为t，则人转过的角度为
| t |
| T0 |
卫星转过的角度为
| t |
| T |
故有
| 2π |
| 3 |
| t |
| T0 |
| t |
| T |
将卫星绕地心运动周期T=2π
|
t=
| TT0 |
| 3(T0-T) |
2π
| ||||
3(T0-2π
|
4π
| ||||
3(T0-4π
|
答：（1）卫星绕地心运动周期T等于4π
|
（2）在赤道上某一点的人能连续看到该卫星的时间是
4π
| ||||
3(T0-4π
|
点评：在地球的质量不知而地球表面的重力加速度已知时，要用黄金代换公式表示地球的质量，这是我们经常使用的方法，要注意掌握．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
