题目内容
【题目】放射性同位素C被考古学家称为“碳钟”，它可以用来判定古生物体的年代，此项研究获得1960年诺贝尔化学奖.
（1）宇宙射线中高能量的中子碰到空气中的氮原子后，会形成很不稳定的 
，它很容易发生衰变，放出β射线变成一个新核，其半衰期为5730年.试写出此核反应方程.
（2）若测得一古生物遗骸中的 含量只有活体中的25%，则此遗骸距今约有多少年？
【答案】
（1）
核反应方程： 
+ 
→ 
+ 
→ + 
.
（2）
活体中的 含量不变，生物死亡后，遗骸中的 按其半衰期变化，设活体中 的含量为N0，遗骸中的 含量为N，由半衰期的定义得：
N=( 
） 
N0即0.25 ) 所以 
=2 t=2τ=11460年 .
【解析】根据电荷数守恒、质量数守恒写出核反应方程；经过一个半衰期，有半数发生衰变，通过剩余的量确定半衰期的次数，从而求出遗骸距今约有多少年
练习册系列答案
相关题目
【题目】某实验小组做“探究弹力和弹簧伸长的关系”的实验．实验时，先把弹簧平放在桌面上，用直尺测出弹簧的原长L0=4.60cm，再把弹簧竖直悬挂起来，在下端挂钩码，每增加一只钩码均记下对应的弹簧的长度x，数据记录如表所示．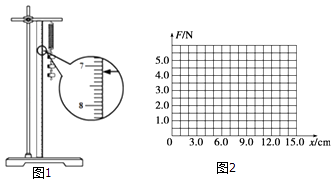
钩码个数 | 1 | 2 | 3 | 4 | 5 |
弹力F/N | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
弹簧的长度x/cm | 9.15 | 11.16 | 13.15 | 15.14 |
（1）根据图1，读出在弹簧下端挂一个钩码时对应的弹簧长度，填入表格 ．
（2）根据表中数据在图2中作出F﹣x图线；
（3）由此图线可得，该弹簧劲度系数k=N/m．
