题目内容
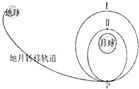
【题目】一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部，另一端和质量为m的小物块a相连，如图所示．质量为 
m的小物块b紧靠a静止在斜面上，此时弹簧的压缩量为x0 ， 从t=0时开始，对b施加沿斜面向上的外力，使b始终做匀加速直线运动．经过一段时间后，物块a、b分离；再经过同样长的时间，b距其出发点的距离恰好也为x0 ． 弹簧的形变始终在弹性限度内，重力加速度大小为g．求
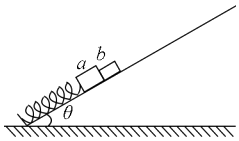
（1）弹簧的劲度系数；
（2）物块b加速度的大小；
（3）在物块a、b分离前，外力大小随时间变化的关系式．
【答案】
（1）
解：对整体分析，根据平衡条件可知，沿斜面方向上重力的分力与弹簧弹力平衡，则有：
kx0=（m+ 
m）gsinθ
解得：k= 
（1）
答：弹簧的劲度系数为 ；
（2）
由题意可知，b经两段相等的时间位移为x0；
由匀变速直线运动相临相等时间内位移关系的规律可知：
= 
（2）
说明当形变量为x1=x0﹣ 
= 
时二者分离；
对m分析，因分离时ab间没有弹力，则根据牛顿第二定律可知：
kx1﹣mgsinθ=ma （3）
联立（1）（2）（3）解得：
a= 
答：物块b加速度的大小为 ；
（3）
设时间为t，则经时间t时，ab前进的位移x= 
at2= 
则形变量变为：△x=x0﹣x
对整体分析可知，由牛顿第二定律有：
F+k△x﹣（m+ m）gsinθ=（m+ m）a
解得：F= 
mgsinθ+ 
因分离时位移x=
由x= = at2解得：
t= 
故应保证t＜ ，F表达式才能成立．
答：在物块a、b分离前，外力大小随时间变化的关系式F= mgsinθ+ （t＜ ）
【解析】（1）对整体分析，根据平衡条件和胡克定律即可求得劲度系数；
（2）分析物体的运动过程，根据运动学规律可明确分离时的位移，从而确定对应的形变量；再根据牛顿第二定律即可求得加速度的大小；
（3）对整体进行分析，根据牛顿第二定律列式即可求得拉力随时间变化的表达式．
名题金卷系列答案
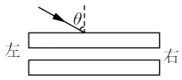
优加精卷系列答案
【题目】某实验小组采用如图所示的装置探究功与速度变化的关系，图中小车中可放置砝码，实验中，打点计时器的工作频率为50 Hz.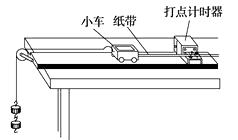
（1）实验的部分步骤如下：
①在小车中放入砝码，把纸带穿过打点计时器，连在小车后端，用细线连接小车和钩码；
②将小车停在打点计时器附近， ， ， 小车拖动纸带，打点计时器在纸带上打下一系列点，；
③改变钩码或小车中砝码的数量，更换纸带，重复②的操作.
（2）如图是钩码质量为0.03 kg、砝码质量为0.02 kg时得到的一条纸带，在纸带上选择起始点O及A、B、C、D、E计数点，可获得各计数点到O的距离x及对应时刻小车的瞬时速度v，请将C点的测量结果填在表中的相应位置.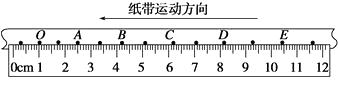
纸带的测量结果
测量点 | x/cm | v/（m·s－1） |
O | 0.00 | 0.35 |
A | 1.51 | 0.40 |
B | 3.20 | 0.45 |
C | ||
D | 7.15 | 0.53 |
E | 9.41 | 0.60 |
（3）本实验，若用钩码的重力表示小车受到的合外力，为了减小这种做法带来的实验误差，应采取的两项措施是：
①；
②.
