题目内容
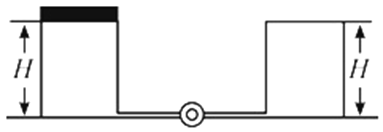
【题目】如图所示，两个截面积都为S的圆柱形容器，右边容器高为H，上端封闭，左边容器上端是一个可以在容器内无摩擦滑动的质量为M的活塞。两容器由装有阀门的极细管道相连，容器、活塞和细管导热性良好。左、右两边容器中装有相同的理想气体，开始时阀门打开，平衡时活塞到容器底的距离为H。现将阀门关闭，在活塞上放一个质量也为M的砝码，活塞缓慢下降，直至系统达到新的平衡。已知外界温度恒定，外界大气压强为
，重力加速度为g，
。
求：(1)当系统达到新的平衡时，活塞距底端的高度；
(2)当系统达到平衡后再打开阀门，活塞又缓慢下降，直到系统再次达到平衡，求左边气体通过阀门进入右边容器的质量与右边气体原有质量的比值。
【答案】(1)
(2) 
【解析】
(1)以左边气体为研究对象，活塞上未放物体前
气体压强
、体积
放上物体后
气体压强
、体积
由玻意耳定律得：
代入数据解得：
(2)以右边封闭气体为研究对象，设气体压强与左边相等时气柱高为
由玻意耳定律得：
代入数据解得：
根据几何关系得左边气体通过阀门进入右边容器的质量与右边气体原来质量的比值
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
