Question

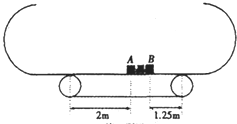
【题目】如图所示，两小物块A、B之间夹着一压缩的轻弹簧，弹簧的弹性势能为EP=12J，开始时，两物体用细线绑着静止在水平传送带上，传送带两端与光滑水平台面相切．已知A的质量m1=1kg，B的质量m2=2kg，A、B距传送带两端的距离分别为2m和1.25m．两物块均可看成质量，且与传送带间的动摩擦因数均为0.2．某一时刻烧断细线，同时传送带以v=3m/s的恒定速度沿顺时针方向运动（忽略传送带加速和弹簧弹开的时间）．取g=10m/s2．

(1)求弹开后瞬间两物体的速度大小；

(2)求两物体到达传送带两端时的速度大小；

(3)若在传送带两端外的水平台面上各固定放置一半径相同的光滑竖直半圆轨道，轨道最低点与水平台面相切，要使两物体第一次冲上内圆轨道后不会脱离轨道，圆轨道的半径应满足什么条件？

Answer 1

【答案】（1）vA=4m/s，vB=2m/s （2）m/s ，3m/s （3）轨道半径大于或等于0.45m

【解析】

(1)对A、B、弹簧的系统在弹开过程，规定向右为正方向：

动量守恒：0=m1vA-m2vB

能量守恒:EP=m1vA2+m2vB2

代入数据得：vA=4m/s，vB=2m/s

(2)弹开后B做加速运动，设B一直加速到右端，由动能定理有：μm2glB=m2vB′2-m2vB2

代入数据得：vB′=3m/s

弹开后A做减速运动，设一直减速到左端：-μm1glA=m1vA′2-m1vA2

代入数据得：vA′=2m/s

(3)欲使AB均不脱离轨道，即均不超过圆心等高处，设恰到圆心等高处：mv2=mgR

解得：R=

因vA′＜vB′

故取vB′，代入数据得：R==0.45m

故轨道半径大于或等于0.45m．