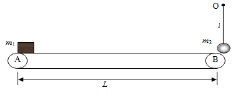题目内容
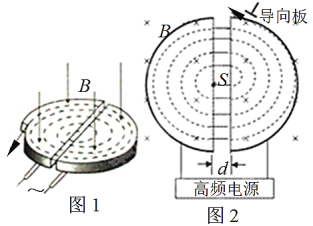
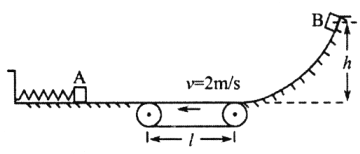
【题目】如图所示，装置的左边是足够长的光滑水平面，一轻质弹簧左端固定，右端连接着质量m=lkg的小物块A，弹簧压缩后被锁定在某一长度。装置的中间是水平传送带，它与左右两边的台面等高，并能平滑对接。传送带始终以v=2ms的速度逆时针转动。装置的右边是一光滑的曲面，质量M=2kg的小物块B从其上距水平台面h=1.0m处由静止释放。已知物块B与传送带之间的动摩擦因数μ=0.2，l=1.0m。设物块A、B之间发生的是对心碰撞(碰撞时间极短)，碰撞后两者一起向前运动且碰撞瞬间弹簧锁定被解除。取g=10m/s2。
(1)求物块B与物块A第一次碰撞前的速度大小；
(2)若物块B第一次与A分离后，恰好运动到右边曲面距水平台面h′=0.5m高的位置，求弹簧被锁定时弹性势能的大小；
(3)在满足(2)问条件的前提下，两物块发生多次碰撞，且每次碰撞后分离的瞬间物块A都会立即被锁定，而当它们再次碰撞前锁定被解除，求物块A、B第n次碰撞后瞬间速度大小。(计算结果可用根号表示)
【答案】（1）物块B与物块A第一次碰撞前的速度大小为
；（2）
；（3）
，
【解析】
（1）B从最高点运动到传送带最左端的过程中，根据动能定理列式求解物块B与物块A第一次碰撞前的速度大小；（2）根据动量守恒定律求解两物体碰后的共同速度；AB及弹簧系统由第一次解锁位置到第一次恢复原长位置，由能量关系求解弹簧被锁定时弹性势能；（3）分析两物块多次碰撞的物理过程，结合能量关系和动量守恒定律，联系数学知识归纳物块A、B第n次碰撞后瞬间速度大小.
（1）若B在传送带上能一直减速运动，设它在最左端时的速度为v1前，则B从最高点运动到传送带最左端的过程中由动能定理：
解得v前1=4m/s>2m/s，则物块B与物块A第一次碰撞前的速度大小为4m/s；
（2）设B与A碰撞后瞬间的共同速度为v1后，对AB系统由动量守恒定律：
分析可知，当弹簧恢复原长时AB分离，设B第一次离开弹簧时速度为v1离，对B离开弹簧到运动到h＇高度处由动能定理：
对AB及弹簧系统由第一次解锁位置到第一次恢复原长位置，由能量守恒定律：
联立解得：
（3）若B从h＇处下落后再传送带上能够一直减速，则B从h＇运动到传送带最左端过程中由动能定理：
解得
，故物块B与物块A第二次碰撞前的速度大小为
；B与A第二次碰撞的过程中，对AB系统：
解得
；
B向右再次冲到传送带上若能在其上速度减为0，设其通过的位移为x，由动能定理：
解得
故而B第三次与A相碰时速度仍为
；
再由：
解得
；
推理可知B与A第n次碰撞后速度大小表达式为：
根据以上分析可知：，（n=2，3，4…）
