题目内容
 长度为L的细线下挂一个质量为m的小球,小球半径忽略不计,现用一个水平力F拉小球使悬线偏离竖直方向θ角并保持静止状态,如图所示
长度为L的细线下挂一个质量为m的小球,小球半径忽略不计,现用一个水平力F拉小球使悬线偏离竖直方向θ角并保持静止状态,如图所示
(1)求拉力F的大小;
(2)撤掉F后,小球从静止开始运动到最低点时的速度为多大?绳子拉力为多少?
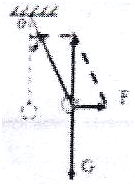 解:(1)小球处于静止状态,合外力为零,对其进行受力分析,
解:(1)小球处于静止状态,合外力为零,对其进行受力分析,如图所示:F=mgtanθ.
(2)根据机械能守恒定律:
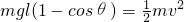
v=
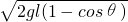
拉力与重力的合力提供向心力:T-mg=
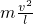 ,
,则T=3mg-2mgcosθ.
答:(1)拉力F的大小为mgtanθ.
(2)小球从静止开始运动到最低点时的速度为
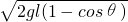 ,绳子的拉力为3mg-2mgcosθ.
,绳子的拉力为3mg-2mgcosθ.分析:(1)小球受重力、绳子的拉力和水平力作用处于静止,根据共点力平衡,运用合成法求出拉力F的大小.
(2)根据机械能守恒定律求出小球运动到最低点的速度,再根据牛顿第二定律求出绳子的拉力大小.
点评:解决本题的关键能够正确地受力分析,运用共点力平衡、机械能守恒定律和牛顿第二定律进行求解.

练习册系列答案
相关题目
 如图所示,弹簧上端固定在O点,下端挂一木匣A,木匣A顶部悬挂一木块B(可当作质点),A和B的质量都为m=1kg,B距木匣底面h=16cm,当它们都静止时,弹簧长度为L,某时刻,悬挂木块B的细线突然断开,在木匣上升到速度刚为0时,B和A的底面相碰,碰撞后结为一体,当运动到弹簧长度又为L时,速度变为v′=1m/s.求:
如图所示,弹簧上端固定在O点,下端挂一木匣A,木匣A顶部悬挂一木块B(可当作质点),A和B的质量都为m=1kg,B距木匣底面h=16cm,当它们都静止时,弹簧长度为L,某时刻,悬挂木块B的细线突然断开,在木匣上升到速度刚为0时,B和A的底面相碰,碰撞后结为一体,当运动到弹簧长度又为L时,速度变为v′=1m/s.求: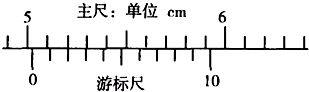 (1)用10分度的游标卡尺测一工件的长度,测得结果如图所示.则该工件的长度L=
(1)用10分度的游标卡尺测一工件的长度,测得结果如图所示.则该工件的长度L=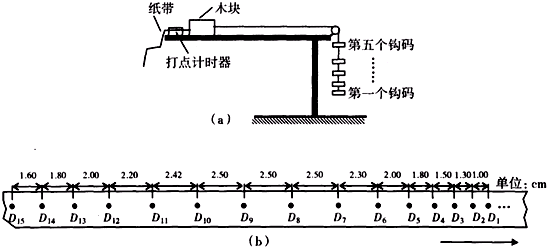



 (1)用10分度的游标卡尺测一工件的长度,测得结果如图所示.则该工件的长度L=______cm.
(1)用10分度的游标卡尺测一工件的长度,测得结果如图所示.则该工件的长度L=______cm.

 在逐渐增大,所以“力越小速度就越小”的观点是不正确的.
在逐渐增大,所以“力越小速度就越小”的观点是不正确的.