��Ŀ����
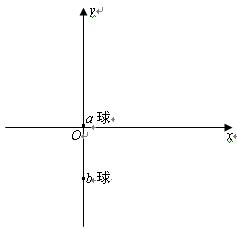
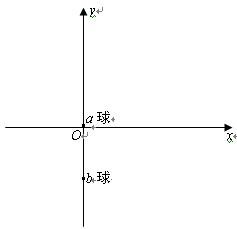
 �ڹ⻬��Եˮƽ���Ͻ�����ͼ��ʾֱ������ϵxoy����y�Ḻ���������������ֱ���µ���ǿ�ų�B=10T����y�����������������ƽ����y�Ტ��+y�����ˮƽ��ǿ�糡���糡ǿ�ȴ�СE=100V/m������һ����m=0.1kg�������q=0.05C�ĸ������Գ��ٶ�v0=10m/s��y���ϵ�P��ƽ����x�Ტ��+x����������ҵ�һ�θպþ���x���ϵ�D�㣮��֪O��P�����l=3m����
�ڹ⻬��Եˮƽ���Ͻ�����ͼ��ʾֱ������ϵxoy����y�Ḻ���������������ֱ���µ���ǿ�ų�B=10T����y�����������������ƽ����y�Ტ��+y�����ˮƽ��ǿ�糡���糡ǿ�ȴ�СE=100V/m������һ����m=0.1kg�������q=0.05C�ĸ������Գ��ٶ�v0=10m/s��y���ϵ�P��ƽ����x�Ტ��+x����������ҵ�һ�θպþ���x���ϵ�D�㣮��֪O��P�����l=3m������1��O��D����֮��ľ���S��
��2�������ڴų����˶��Ĺ���뾶R��
��3�����ɴ�P��������ڶ��ξ���x���ʱ��t��
��������1���ٶȷ�����糡����ֱ������ڵ糡������ƽ���˶����ڵ糡�����������ٶ�Ϊ����ȼ���ֱ���˶����ڴ�ֱ�ڵ糡�ķ�����������ֱ���˶���Ӧ����ƽ���˶���֪ʶ����⣮
��2�������������ƽ���˶�����ٶȴ�С��Ȼ����ݴų���Բ���˶��İ뾶��ʽ��R��
��3����ƽ���˶���ʱ����ų����˶�ʱ��֮�ͼ�Ϊ����
��2�������������ƽ���˶�����ٶȴ�С��Ȼ����ݴų���Բ���˶��İ뾶��ʽ��R��
��3����ƽ���˶���ʱ����ų����˶�ʱ��֮�ͼ�Ϊ����
����⣺��1�������ڵ糡����ļ��ٶȣ�a=
=50m/s2
��l=
at2 �ã�t=
=
s
S=v0t
�ã�S=2
m
��2��vy=at=10
m/s
v0=10m/s
����ٶ�v=20m/s
R=
=4m
��3�������ӽ���ų�ʱ��x��н�Ϊ��
tan��=
=
���=60��
�������ڴų����˶���Բ�Ľ�Ϊ120��
T=
=0.4��s
�������ڴų����˶���ʱ��t��=
T=
s
t=
+
=
s
�𣺣�1��O��D����֮��ľ���SΪ2
m��
��2�������ڴų����˶��Ĺ���뾶RΪ4m��
��3�����ɴ�P��������ڶ��ξ���x���ʱ��tΪ
s��
| qE |
| m |
��l=
| 1 |
| 2 |
|
| ||
| 5 |
S=v0t
�ã�S=2
| 3 |
��2��vy=at=10
| 3 |
v0=10m/s
����ٶ�v=20m/s
R=
| mv |
| qB |
��3�������ӽ���ų�ʱ��x��н�Ϊ��
tan��=
| vy |
| v0 |
| 3 |
�������ڴų����˶���Բ�Ľ�Ϊ120��
T=
| 2��m |
| qB |
�������ڴų����˶���ʱ��t��=
| 120�� |
| 360�� |
| 2�� |
| 15 |
t=
| ||
| 5 |
| 2�� |
| 15 |
3
| ||
| 15 |
�𣺣�1��O��D����֮��ľ���SΪ2
| 3 |
��2�������ڴų����˶��Ĺ���뾶RΪ4m��
��3�����ɴ�P��������ڶ��ξ���x���ʱ��tΪ
3
| ||
| 15 |
���������⿼������������ϳ��е��˶���һֱ���ѵ����⣬Ҫ���������ڵ糡��ƫת���Լ����ٶȵ���ⷽ����

��ϰ��ϵ�д�
 ͬ��������ϰϵ�д�
ͬ��������ϰϵ�д� �ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�ο�ͨ�γ̱�˼ά����������ѵ��ϵ�д�
�����Ŀ
 ��2010?ɽ��ģ�⣩�ڹ⻬��Ե��ˮƽ���Ͻ�����ͼ��ʾ��ƽ��ֱ������ϵ���ڴ�ˮƽ���Ͽ���Ϊ�ʵ�IJ�����С��a��ֹ������ϵ��ԭ��O������Ϊ�ʵ�Ĵ�����С��b��ֹ������Ϊ��0��-h����λ���ϣ��ּ�һ������y�������糡ǿ�ȴ�СΪE����Χ�㹻�����ǿ�糡��ͬʱ��a����ijһ�ٶ�ʹ����x���������˶�����b������ϵԭ��Oʱ�ٶ�Ϊv0����ʱ������ȥ�糡���ļ�һ����ֱ�ھ�Եˮƽ�����ϡ��Ÿ�Ӧǿ�ȴ�СΪB����Χ�㹻�����ǿ�ų�������b������a����������
��2010?ɽ��ģ�⣩�ڹ⻬��Ե��ˮƽ���Ͻ�����ͼ��ʾ��ƽ��ֱ������ϵ���ڴ�ˮƽ���Ͽ���Ϊ�ʵ�IJ�����С��a��ֹ������ϵ��ԭ��O������Ϊ�ʵ�Ĵ�����С��b��ֹ������Ϊ��0��-h����λ���ϣ��ּ�һ������y�������糡ǿ�ȴ�СΪE����Χ�㹻�����ǿ�糡��ͬʱ��a����ijһ�ٶ�ʹ����x���������˶�����b������ϵԭ��Oʱ�ٶ�Ϊv0����ʱ������ȥ�糡���ļ�һ����ֱ�ھ�Եˮƽ�����ϡ��Ÿ�Ӧǿ�ȴ�СΪB����Χ�㹻�����ǿ�ų�������b������a����������