题目内容
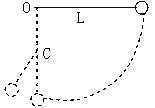
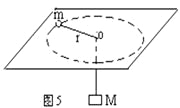
【题目】一半径为R的圆筒的横截面如图所示，其圆心为0。筒内有垂直于纸面向里的匀强磁场，磁感应强度为
(未知)。质量为m、电荷量为+q的粒子以速度v从小孔S沿半径SO方向射入磁场中，粒子与圆简壁发生两次磁撞后仍从S孔射出。(粒子重力不计，粒子与圆筒壁碰撞没有能量损失，且电量保持不变；
，
，
）
(1)求磁感应强度B的大小。
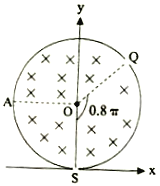
(2)若改变磁场的大小，使
，且在圆筒上开一小孔Q，圆弧SQ对应的圆心角为0.8π，如图所示，其它条件不变。求粒子从S孔射入到从Q孔射出的过程中与简壁碰撞的次数。
(3)若圆筒内的磁场改为与圆筒横截面平行的匀强电场，电场强度
，其它条件不变，则从S孔射入的粒子会打在四分之一圆弧的A点且速度大小为2v，现以S点为坐标原点，建立直角坐标系，如图所示。令A点为零电势点，求圆筒的横截面上电势最高点的坐标(x，y)和最高电势
的值。
【答案】(1)
(2)碰3次。(3) 电势最高点G的坐标：
【解析】试题分析（1）根据题意作出粒子在磁场中运动的轨迹图，根据几何关系求出半径，根据洛伦兹力提供向心力求出磁感应强度；（2）根据洛伦兹力提供向心力求出粒子运动的半径，再根据题目要求出碰撞的次数；（3）根据动能定理和带电粒子在电场中运动的特点即可求解。
(1)粒子进入磁场后做匀速圆周运动，圆心
，圆半径为r，运动轨迹如图
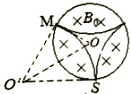
设第一次碰撞点为M，由于粒子与圆筒发生两次碰撞又从S孔射出，因此SM弧所对圆心角
由几何关系得
，得
R
粒子运动过程中洛伦兹力充当向心力，由牛顿第二定律，得
联立得磁感应强度为
(2)若取
，粒子运动过程中洛伦兹力提供向心力，由牛顿第二定律，得
联立得r=3.08R
依题给条件得θ=0.4π，设粒子在圆筒中发生n碰撞转k周后从Q孔射出
则应满足：
故从S孔射出时k=2，n=3 既碰3次。
(3)连接SA，如图所示
设S到A沿电场方向的距离为d，由动能定理：
得：
由于
，可知∠SAC为30.电场线与SC所在直线平行，方向由S指向C
过O点作SC的平行线与圈环交于G、F点，由几何关系可知：
电势最高点G的坐标：
所以
解得：
【题目】科学探究活动通常包括以下环节：提出问题，作出假设，制定计划，搜集证据，评估交流等．一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下
A．有同学认为：运动物体所受空气阻力可能与其运动速度有关
B．他们计划利用一些“小纸杯”作为研究对象，用超声测距仪等仪器测量“小纸杯”在空中直线下落时的下落距离、速度随时间变化的规律，以验证假设
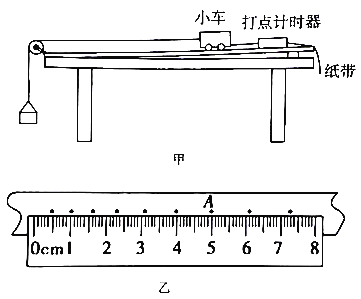
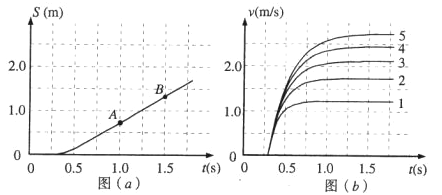
C．在相同的实验条件下，同学们首先测量了单只“小纸杯”在空中下落过程中不同时刻的下落距离，将数据填入表中，如图（a）是对应的位移—时间图线．然后将不同数量的“小纸杯”叠放在一起从空中下落，分别测出它们的速度—时间图线，如图（b）中图线1、2、3、4、5所示
D.同学们对实验数据进行分析、归纳后，证实了他们的假设．
回答下列提问：
（1）与上述过程中A、C步骤相应的科学探究环节分别是________、________；
（2）图（a）中的AB段反映了运动物体在做________运动，表中x处的值为________；
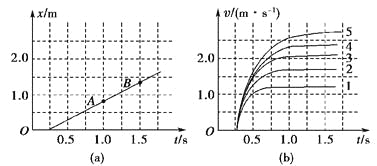（3）图（b）中各条图线具有共同特点，“小纸杯”在下落的开始阶段做__________运动，最后“小纸杯”做________运动；
时间（s） | 下落距离（m） |
0.0 | 0.000 |
0.4 | 0.036 |
0.8 | 0.469 |
1.2 | 0.957 |
1.6 | 1.447 |
2.0 | x |
