题目内容
如图所示,绝缘轨道平面与水平面垂直,倾斜轨道部分摩擦因数μ=0.2,倾斜轨道与水平面夹角θ=37°,倾斜轨道足够长与半径R=0.5m的半圆形光滑轨道圆滑连接,整个轨道处在水平向左的匀强电场中,电场强度E=10V/m,一带负电的小物块质量为0.3kg所带电量为0.4C,让小物块在倾斜轨道上从与半圆轨道最高点C点等高的A点由静止释放.(重力加速度g=10m/s2,sin37°=
,cos37°=
,此题结果可用分数表示)
求:(1)小物块在半圆轨道上运动过场中的最大动能?
(2)使小物块恰好通过半圆轨道最高点C处,将其在倾斜轨道上由静止释放时距水平面的高度H?
(3)在(2)中小物块通过C点时,电场立即消失,小物块打在倾斜轨道上的位置距地面的高度h?

| 3 |
| 5 |
| 4 |
| 5 |
求:(1)小物块在半圆轨道上运动过场中的最大动能?
(2)使小物块恰好通过半圆轨道最高点C处,将其在倾斜轨道上由静止释放时距水平面的高度H?
(3)在(2)中小物块通过C点时,电场立即消失,小物块打在倾斜轨道上的位置距地面的高度h?

分析:本题(1)的难点是找到小物块在半圆轨道上速度最大的位置是小物块受到的电场力与重力的合力反向延长线应过半圆轨道的圆心,以及分析得出小物块在倾斜轨道上运动时正好不受摩擦力,然后根据动能定理即可求解.(2)题的关键是抓住小物块恰好通过半圆轨道最高点C时应满足mg=
的条件,然后再用动能定理即可求解.(3)题的关键是撤去电场后小物块将做平抛运动,根据平抛运动处理方法即可求解.
| ||
| R |
解答:解:(1)令小物块动能最大的位置为D点,分析得:
当电场力与重力的合力反向延长线过半圆轨道圆心时,
小物块动能最大,设合力与竖直方向的夹角为α,则有tanα=
=
,即α=53°
小物块在倾斜轨道上时,因为mgcosθ=Eqsinθ
所以小物块与倾斜轨道间无摩擦
对小物块从A→D由动能定理:mg(R+Rcosα)+Eq(
+Rsinα)=Ek-0
代入数据解得:Ek=
J
故小物块在半圆轨道上运动过场中的最大动能为
J.
(2)小物块恰好通过最高处C点,有mg=m
①
从释放点到C点由动能定理mg(H-2R)+Eq
=
m
②
①②式联立解得:H=
m
故使小物块恰好通过半圆轨道最高点C处,将其在倾斜轨道上由静止释放时距水平面的高度H=
m.
(3)小物块离开C点后做平抛运动2R-h=
gt2,
=vct
整理有:16h2+9h-9=0
解得:h1=
,h2=
(舍)
故小物块打在倾斜轨道上的位置距地面的高度h为
m.
当电场力与重力的合力反向延长线过半圆轨道圆心时,
小物块动能最大,设合力与竖直方向的夹角为α,则有tanα=
| Eq |
| mg |
| 4 |
| 3 |
小物块在倾斜轨道上时,因为mgcosθ=Eqsinθ
所以小物块与倾斜轨道间无摩擦
对小物块从A→D由动能定理:mg(R+Rcosα)+Eq(
| 2R |
| tanθ |
代入数据解得:Ek=
| 28 |
| 3 |
故小物块在半圆轨道上运动过场中的最大动能为
| 28 |
| 3 |
(2)小物块恰好通过最高处C点,有mg=m
| ||
| R |
从释放点到C点由动能定理mg(H-2R)+Eq
| H |
| tanθ |
| 1 |
| 2 |
| v | 2 c |
①②式联立解得:H=
| 9 |
| 20 |
故使小物块恰好通过半圆轨道最高点C处,将其在倾斜轨道上由静止释放时距水平面的高度H=
| 9 |
| 20 |
(3)小物块离开C点后做平抛运动2R-h=
| 1 |
| 2 |
| h |
| tanθ |
整理有:16h2+9h-9=0
解得:h1=
-9+
| ||
| 32 |
-9-
| ||
| 32 |
故小物块打在倾斜轨道上的位置距地面的高度h为
-9+
| ||
| 32 |
点评:遇到与圆周运动结合的题目时,注意寻找物体运动速度最大与最小位置的方法:先找出物体能够静止的位置(平衡位置)即为最大速度时的位置,然后再找到该点关于圆心的对称点即为最小速度的位置(等效最高点).

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
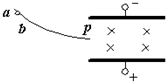 如图所示,带电平行板中匀强电场竖直向上,匀强磁场方向垂直纸面向里,某带电小球从光滑绝缘轨道上的a点滑下,经过轨道端点P进入板间后恰好沿水平方向做直线运动,现使小球从稍低些的b点开始自由滑下,在经过P点进入板间的运动过程中( )
如图所示,带电平行板中匀强电场竖直向上,匀强磁场方向垂直纸面向里,某带电小球从光滑绝缘轨道上的a点滑下,经过轨道端点P进入板间后恰好沿水平方向做直线运动,现使小球从稍低些的b点开始自由滑下,在经过P点进入板间的运动过程中( )| A、速度会减小 | B、其电势能将会增大 | C、受的洛伦兹力增大 | D、小球将做类平抛运动 |
 如图所示,在竖直的xOy平面上,有一根绝缘光滑的抛物线型硬杆,抛物线方程为y=kx2,其中k为正常数.空间中有沿x轴正向的匀强电场.一个套在杆上带正电的小环在轨道的A点由静止开始滑下,轨道上的B点与A点关于y轴对称.对于带电小环的下列说法,正确的是( )
如图所示,在竖直的xOy平面上,有一根绝缘光滑的抛物线型硬杆,抛物线方程为y=kx2,其中k为正常数.空间中有沿x轴正向的匀强电场.一个套在杆上带正电的小环在轨道的A点由静止开始滑下,轨道上的B点与A点关于y轴对称.对于带电小环的下列说法,正确的是( )



