题目内容
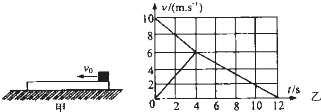
如图甲所示，一长木板，静止放置在粗糙水平地面上，有一个可视为质点的物块，以某一水平初速度v0从右端冲上木板，从物块冲上木板到物块和木板达到共同速度的过程中，物块和木板的v-t 图象如图乙所示．已知物块与木板间的动摩擦因数为μ1，木板与地面间的动摩擦因数为μ2，g取10m/s2，求
（1）μ1与μ2的比值；
（2）物块相对木板滑行的距离△x．
（1）μ1与μ2的比值；
（2）物块相对木板滑行的距离△x．
分析：（1）v-t图象中，倾斜的直线表示匀变速直线运动，斜率表示加速度；结合牛顿第二定律列式即可求得μ1与μ2的比值；
（2）图象与坐标轴围成的面积表示位移，由v-t图可以看出，物块相对于长木板滑行的距离△x对应图中图象与坐标轴围成的面积之差．
（2）图象与坐标轴围成的面积表示位移，由v-t图可以看出，物块相对于长木板滑行的距离△x对应图中图象与坐标轴围成的面积之差．
解答：解：（1）由v-t图象可求出物块冲上木板做匀减速直线运动的加速度大小a1=
m/s2=1 m/s2，
木板开始做匀加速直线运动的加速度大小a2=
m/s2=1.5 m/s2，
达到同速后一起匀减速运动的加速度大小a3=
=
=0.75 m/s2．
对m冲上木板减速阶段：μ1mg=ma1
解得：μ1=0.1
物块和木板达到共同速度后向前减速阶段：μ2（m+M）g=（M+m）a3
解得：μ2=0.075
所以
=
=
．
（3）由v-t图可以看出，物块相对于长木板滑行的距离△s对应图中左边三角形的面积，故△x=10×4×
m=20 m
答：（1）μ1与μ2的比值为4：3；（2）物块相对木板滑行的距离△x为20m．
| 10-6 |
| 4 |
木板开始做匀加速直线运动的加速度大小a2=
| 6-0 |
| 4 |
达到同速后一起匀减速运动的加速度大小a3=
| 6-0 |
| 8 |
| 3 |
| 4 |
对m冲上木板减速阶段：μ1mg=ma1
解得：μ1=0.1
物块和木板达到共同速度后向前减速阶段：μ2（m+M）g=（M+m）a3
解得：μ2=0.075
所以
| μ1 |
| μ2 |
| 0.1 |
| 0.075 |
| 4 |
| 3 |
（3）由v-t图可以看出，物块相对于长木板滑行的距离△s对应图中左边三角形的面积，故△x=10×4×
| 1 |
| 2 |
答：（1）μ1与μ2的比值为4：3；（2）物块相对木板滑行的距离△x为20m．
点评：本题是速度--时间图象的应用，要明确斜率的含义，知道在速度--时间图象中图象与坐标轴围成的面积的含义，能根据图象读取有用信息．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
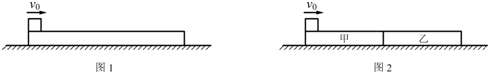
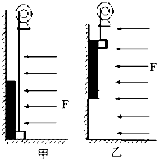如图甲所示，一长绝缘木板靠在光滑竖直墙面上，质量为m=1kg．木板右下方有一质量为2m的小滑块（可视为质点），滑块与木板间的动摩擦因数为μ=0.4，木板与滑块处有恒定的风力F=4mg，风力方向水平向左，若电动机通过一根绝缘绳拉动滑块（绳保持竖直），使之从地面由静止开始匀加速向上移动，当滑块与木板分离时（如图乙所示），滑块的速度大小为v=8m/s，此过程中电动机对滑块做的功为W0=136J（重力加速度为g=10m/s2）．
