题目内容
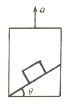
【题目】在工厂的流水线上安装有传送带，用传送带传送工件，可大大提高工作效率．如图所示，传送带与水平面夹角为θ＝30°，其上、下两端点A、B间的距离是3.84 m．传送带在电动机的带动下，以4.0 m/s顺时针匀速运转．现将质量为10 kg的工件(可视为质点)轻放于传送带的A点，已知工件与传送带间的动摩擦因数为
，则在传送带将工件从A点传送到B点过程中，g取10 m/s2.
(1)求工件放上传送带时的加速度大小．
(2)当工件与传送带速度相等时，传送带立即以8 m/s2的加速度顺时针匀减速运转，求此时工件的摩擦力大小及工件从A点传送到B点的时间．
(3)若传送带因故障被卡住，要使静止工件以(1)问的加速度从A点运动到B点，则需对工件提供的最小拉力为多少？
【答案】（1）
（2）
（3）
【解析】
试题分析:（1）工件无初速度放于传送带上，由牛顿第二定律：
（2分）
可得：
（2分）
（2）等速后，假设物体与传送带一起减速，则有
（2分）
得：
，假设成立，摩擦力方向沿斜面向下 （2分）
匀加速过程：时间
位移
（1分）
匀减速过程：
得：
或
（舍去） (2分)
全程：
(1分)
（3）设拉力
斜向上，与斜面的夹角为
，则有:
（2分）
（2分）
两式化简：
即
力的最小值
，代数据得：
（1分）
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
