题目内容
【题目】一个带正电荷的小球，质量为m，电荷量为q，从光滑绝缘的斜面轨道的A点由静止下滑，小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动，现在竖直方向上加如图所示的匀强电场，若仍从A点由静止释放该小球，则
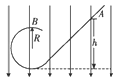
A、小球不能过B点
B、小球仍恰好能过B点
C、小球能过B点，且在B点与轨道之间压力不为零
D、以上说法都不对
【答案】B
【解析】
试题分析：当没有施加电场前，小球恰好能通过B点，则在B点重力完全充当向心力，根据牛顿第二定律可得
，解得
，小球从A点释放后，由于只有重力做功，所以过程中机械能守恒，所以
，解得
，当施加电场后，如果小球仍恰好通过B点，则在B点重力和电场的合力充当向心，即
，解得
，从A点释放后到B点过程中，根据动能定理可得
，解得
，即小球恰好能通过B点，ACD错误B正确；
练习册系列答案
名校课堂系列答案
相关题目
【题目】某同学在“研究匀变速直线运动”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点，其相邻两点间的距离如图甲所示，每两个相邻的计数点之间的时间间隔均为0.10s。
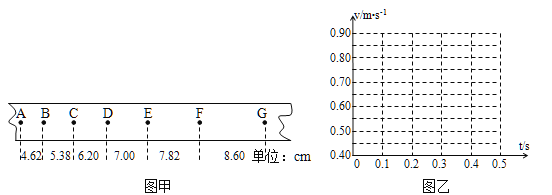
（1）试根据纸带上各个计数点间的距离，计算打下B、C、D、E、F五个点时小车的瞬时速度，请将D点的速度值填在下面的表格内（保留到小数点后两位）；
计数点序号 | B | C | D | E | F |
计数点对应的时刻t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
通过计数点时小车的速度v/ms﹣1 | 0.50 | 0.58 | 0.74 | 0.82 |
（2）以A点为计时零点，将B、C、D、E、F各个时刻的瞬时速度标在如图乙所示的坐标纸上，并画出小车的瞬时速度v随时间t变化的关系图线；
（3）根据第（2）问中画出的v﹣t图线，求出小车运动的加速度大小a= m/s2（保留三位有效数字）。
