题目内容
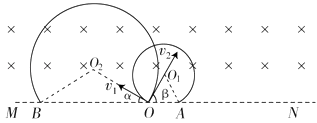
【题目】如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场,质量为m、电荷量为﹣q(q>0)的粒子1在纸面内以速度v1=v0从O点射入磁场,其方向与MN的夹角α=30°;质量为m、电荷量为+q的粒子2在纸面内以速度v2= ![]() v0也从O点射入磁场,其方向与MN的夹角β=60°角.已知粒子1、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用.
v0也从O点射入磁场,其方向与MN的夹角β=60°角.已知粒子1、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用.
(1)求两粒子在磁场边界上的穿出点A、B之间的距离d;
(2)求两粒子进入磁场的时间间隔△t;
(3)若MN下方有平行于纸面的匀强电场,且两粒子在电场中相遇,其中的粒子1做直线运动.求电场强度E的大小和方向.
【答案】
(1)解:粒子在匀强磁场中作匀速圆周运动:
根据牛顿第二定律:qvB=m ![]()
粒子1圆周运动的圆心角θ1= ![]() ,
, ![]() =2r1sinθ1
=2r1sinθ1
粒子2圆周运动的圆心角θ2= ![]() ,
, ![]() =2r2sinθ2
=2r2sinθ2
故d= ![]() +
+ ![]() =2r1sin30°+2r2sin60°=
=2r1sin30°+2r2sin60°= ![]()
答:两粒子在磁场边界上的穿出点A、B之间的距离是 ![]() ;
;
(2)解:粒子圆周运动的周期为:T= ![]()
粒子1在匀强磁场中运动的时间为:t1= ![]() T
T
粒子2在匀强磁场中运动的时间为:t2= ![]() T
T
所以有:△t=t1﹣t2= ![]()
答:两粒子进入磁场的时间间隔是 ![]() ;
;
(3)解:由题意,电场强度的方向应与粒子1穿出磁场的方向平行.
a.若电场强度的方向与MN成30°角斜向右上,则粒子1做匀加速直线运动,粒子2做类平抛运动.
Eq=ma
![]() cos30°=v1t+
cos30°=v1t+ ![]() at2+
at2+ ![]() at2
at2
![]() sin30°=v2t
sin30°=v2t
解得:E= ![]() Bv0
Bv0
b.若电场强度的方向与MN成30°角斜向左下,则粒子1做匀减速直线运动,粒子2做类平抛运动.
Eq=ma
![]() cos30°=v1t﹣
cos30°=v1t﹣ ![]() at2﹣
at2﹣ ![]() at2
at2
![]() sin30°=v2t
sin30°=v2t
解得:E=﹣ ![]() Bv0,假设不成立.
Bv0,假设不成立.
综上所述,电场强度的大小E= ![]() Bv0,方向与MN成30°角斜向右上.
Bv0,方向与MN成30°角斜向右上.
答:若MN下方有平行于纸面的匀强电场,且两粒子在电场中相遇,其中的粒子1做直线运动.电场强度E的大小E= ![]() Bv0,方向与MN成30°角斜向右上.
Bv0,方向与MN成30°角斜向右上.
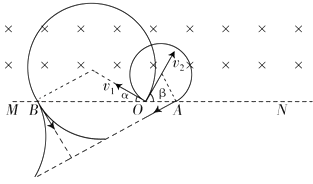
【解析】(1)作出两粒子的运动轨迹,由牛顿第二定律求出半径,结合几何知识求出d;(2)根据公式t= ![]() T求运动时间;(3)由题意,电场强度的方向应与粒子1穿出磁场的方向平行,分为与粒子速度方向相同和相反两种情况进行讨论.
T求运动时间;(3)由题意,电场强度的方向应与粒子1穿出磁场的方向平行,分为与粒子速度方向相同和相反两种情况进行讨论.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】现用频闪照相方法来研究物块的变速运动.在一小物块沿斜面向下运动的过程中,用频闪相机拍摄的不同时刻物块的位置如图所示.拍摄时频闪频率是10Hz;通过斜面上固定的刻度尺读取的5个连续影像间的距离依次为x1、x2、x3、x4.已知斜面顶端的高度h和斜面的长度s.数据如下表所示.重力加速度大小g=9.80m/s2.
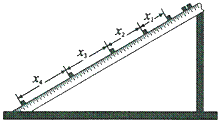
单位:cm
x1 | x2 | x3 | x4 | h | S |
10.76 | 15.05 | 19.34 | 23.65 | 48.00 | 80.00 |
根据表中数据,完成下列填空:
(1)物块的加速度a=_____m/s2(保留3位有效数字).
(2)因为_____可知斜面是粗糙的.