题目内容
如图所示,磁感应强度大小为B="0." 15 T,方向垂直纸面向里的匀强磁场分布在半径R="0.10" m的圆形区域内,圆的左端跟y轴相切于直角坐标系原点O,右端跟荧光屏MN相切于x轴上的A点。置于原点O的粒子源可沿x轴正方向射出速度 =" 3." 0
=" 3." 0 m/s的带正电粒子流,粒子重力不计,比荷为
m/s的带正电粒子流,粒子重力不计,比荷为 =" 1." 0
=" 1." 0 C/kg。现以过O点并垂直于纸面的直线为轴,将圆形磁场逆时针缓慢旋转
C/kg。现以过O点并垂直于纸面的直线为轴,将圆形磁场逆时针缓慢旋转 ,求此过程中粒子打在荧光屏上的范围。
,求此过程中粒子打在荧光屏上的范围。

 =" 3." 0
=" 3." 0 m/s的带正电粒子流,粒子重力不计,比荷为
m/s的带正电粒子流,粒子重力不计,比荷为 =" 1." 0
=" 1." 0 C/kg。现以过O点并垂直于纸面的直线为轴,将圆形磁场逆时针缓慢旋转
C/kg。现以过O点并垂直于纸面的直线为轴,将圆形磁场逆时针缓慢旋转 ,求此过程中粒子打在荧光屏上的范围。
,求此过程中粒子打在荧光屏上的范围。
当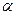 由
由 变化到
变化到 的过程中,
的过程中, 逐渐增大,s也逐渐增大;当
逐渐增大,s也逐渐增大;当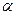 由
由 变化到
变化到 的过程中,
的过程中, 逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。
逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。
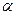 由
由 变化到
变化到 的过程中,
的过程中, 逐渐增大,s也逐渐增大;当
逐渐增大,s也逐渐增大;当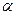 由
由 变化到
变化到 的过程中,
的过程中, 逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。
逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。设粒子在磁场中沿OB弧做匀速圆周运动的半径为r,由牛顿第二定律得


 0.20 m
0.20 m
如图所示,当圆的直径OD转动到与x轴的夹角为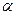 时,粒子从圆形磁场中的B点射出,粒子在磁场中的偏角为
时,粒子从圆形磁场中的B点射出,粒子在磁场中的偏角为 ,打在荧光屏上的点到x轴的距离为s,由几何知识得
,打在荧光屏上的点到x轴的距离为s,由几何知识得
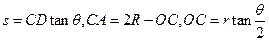
联立解得
代入数据并化简得 m
m
故 最大时,s最大。如图,当D点与出射点B重合时,
最大时,s最大。如图,当D点与出射点B重合时, 最大。由几何知识
最大。由几何知识
 ,得
,得
求得粒子打在荧光屏上最远点到x轴的距离为 ,此时
,此时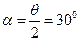
当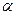 由
由 变化到
变化到 的过程中,
的过程中, 逐渐增大,s也逐渐增大;当
逐渐增大,s也逐渐增大;当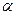 由
由 变化到
变化到 的过程中,
的过程中, 逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。
逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。


 0.20 m
0.20 m如图所示,当圆的直径OD转动到与x轴的夹角为
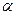 时,粒子从圆形磁场中的B点射出,粒子在磁场中的偏角为
时,粒子从圆形磁场中的B点射出,粒子在磁场中的偏角为 ,打在荧光屏上的点到x轴的距离为s,由几何知识得
,打在荧光屏上的点到x轴的距离为s,由几何知识得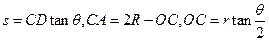
联立解得

代入数据并化简得
 m
m故
 最大时,s最大。如图,当D点与出射点B重合时,
最大时,s最大。如图,当D点与出射点B重合时, 最大。由几何知识
最大。由几何知识 ,得
,得
求得粒子打在荧光屏上最远点到x轴的距离为
 ,此时
,此时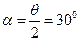
当
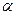 由
由 变化到
变化到 的过程中,
的过程中, 逐渐增大,s也逐渐增大;当
逐渐增大,s也逐渐增大;当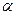 由
由 变化到
变化到 的过程中,
的过程中, 逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。
逐渐减小至零,s也逐渐减小至零.故粒子打在荧光屏上的范围s为0~0. 15 m。
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目

 ,其它电阻不计,ab、cd与滑轨间的动摩擦因数
,其它电阻不计,ab、cd与滑轨间的动摩擦因数 =0.5,问:
=0.5,问:  =10m/s的速度做匀速直线运动?
=10m/s的速度做匀速直线运动? 
 ,一束电荷量相同的带正电的粒子沿电容器的中心线平行于极板射入电容器,沿直线穿过电容器后进入另一磁感应强度为
,一束电荷量相同的带正电的粒子沿电容器的中心线平行于极板射入电容器,沿直线穿过电容器后进入另一磁感应强度为 的匀强磁场,结果分别打在感光片上的a、b两点,设a、b两点间距离为
的匀强磁场,结果分别打在感光片上的a、b两点,设a、b两点间距离为 ,粒子所带电荷量为q,且不计重力,求:
,粒子所带电荷量为q,且不计重力,求:
 。
。 =
= ,上面放着质量为80 g的金属杆ab,整个装置放在B="0.2" T的匀强磁场中。
,上面放着质量为80 g的金属杆ab,整个装置放在B="0.2" T的匀强磁场中。