题目内容

（15分）如图所示，MN与PQ为在同一水平面内的平行光滑金属导轨，间距l=0.5m，电阻不计，在导轨左端接阻值为R=0.6Ω的电阻．整个金属导轨置于竖直向下的匀强磁场中，磁感应强度大小为B=2T．将质量m=1kg、电阻r=0.4Ω的金属杆ab垂直跨接在导轨上．金属杆ab在水平拉力F的作用下由静止开始向右做匀加速运动．开始时，水平拉力为F0=2N．
（1）求金属杆ab的加速度大小；
（2）求2s末回路中的电流大小；
（3）已知开始2s内电阻R上产生的焦耳热为6.4J，求该2s内水平拉力F所做的功．

（1）2 m/s2  （2）4A  （3）18.7J

解析试题分析：（1）（4分）在初始时刻，由牛顿第二定律:          （2分）
得                                （2分）
（2）（5分）2s末时，                           （1分）
感应电动势                                  （2分）
回路电流为                                 （2分）
（3）（6分）设拉力F所做的功为, 由动能定理:      （2分）
为金属杆克服安培力做的总功，它与R上焦耳热关系为： ，（2分）
得：                                           （1分）
所以：                       （1分）
考点：本题考查电磁感应、动能定理

练习册系列答案
相关题目

如图所示，AB为固定在竖直平面内的1/4光滑圆弧轨道，轨道的B点与水平地面相切，其半径为R，质量为m的小球由A点静止释放，试求：

（1）小球滑到最低点B时，小球速度v的大小；
（2）小球刚到达最低点B时，轨道对小球支持力FN的大小；
（3）球通过光滑的水平面BC滑上固定曲面，恰达最高点D，D到地面的高度为h(已知h <R)，则小球在曲面上克服摩擦力所做的功Wf。

如图所示，王鹏以v0=8m/s的速度将质量m=6kg的铅球斜向上抛出，他的出手高度h=1.8m。若忽略空气阻力，取g=10m/s2。求：

（1）铅球在掷出时所具有的重力势能（以地面为参考平面）；
（2）铅球在掷出时的动能；
（3）铅球落地时的速度大小。

（12分） 以v0=20m/s的初速度，从地面竖直向上抛出一质量为m=5kg物体，物体落回地面时的速度大小为v=10m/s。如果物体在运动过程中所受阻力的大小不变，且和地面碰后不再反弹 （以地面为重力零势能面，g=10m/s2），求：
（1）物体运动过程中所受阻力的大小；
（2）物体在离地面多高处，物体的动能与重力势能相等。

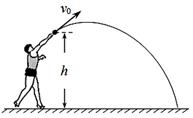
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点，随传送带运动到A点后水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑的圆弧轨道下滑。B、C为圆弧的两端点，其连线水平。已知圆弧半径R=1.0m圆弧对应圆心角，轨道最低点为O，A点距水平面的高度h=0.8m,小物块离开C点后恰能无碰撞的沿固定斜面向上运动，0.8s后经过D点，物块与斜面间的动摩擦因数为 （g=10m/s2，sin37°=0.6,cos37°=0.8）试求：

（1）小物块离开A点时的水平初速度v1；
（2）小物块经过O点时对轨道的压力； 
（3）假设小物块与传送带间的动摩擦因数为0.3，传送带的速度为5m/s，则PA间的距离是多少？（用动能定理解答）
（4）斜面上CD间的距离。

（20分）如下图是阿毛同学的漫画中出现的装置，描述了一个“吃货”用来做“糖炒栗子”的“萌”事儿：将板栗在地面小平台上以一定的初速经两个四分之一圆弧衔接而成的轨道，从最高点P飞出进入炒锅内，利用来回运动使其均匀受热。我们用质量为m的小滑块代替栗子，借这套装置来研究一些物理问题。设大小两个四分之一圆弧半径为2R和R，小平台和圆弧均光滑。将过锅底的纵截面看作是两个斜面AB、CD和一段光滑圆弧组成。斜面动摩擦因数均为0.25，而且不随温度变化。两斜面倾角均为，AB=CD=2R，A、D等高，D端固定一小挡板，碰撞不损失机械能。滑块的运动始终在包括锅底最低点的竖直平面内，重力加速度为g.

（1）如果滑块恰好能经P点飞出，为了使滑块恰好沿AB斜面进入锅内，应调节锅底支架高度使斜面的A、D点离地高为多少？
（2）接（1）问，求滑块在锅内斜面上走过的总路程。
（3）对滑块的不同初速度，求其通过最高点P和小圆弧最低点Q时受压力之差的最小值。

质量为m、电量为-q的带电粒子，从图中的O点以初速度v0射入场强为E的匀强电场中，v0与x轴方向夹角为θ，飞出电场时速度恰好沿y轴的正方向(与电场垂直).设粒子在电场中仅受电场力作用，在这过程中，带电粒子动量的增量大小为______，动能增量为______.

(12分) 如图所示，粗糙程度均匀的绝缘斜面倾角为θ。其下方O点处有一固定的正点电荷，电荷量为Q，OD⊥MN，OM=ON，质量为m、带负电的小滑块以初速度v1从M点沿斜面上滑，到达N点时速度恰好为零，然后又滑回到M点，速度大小变为v2。若小滑块带电量大小为q且保持不变，可视为点电荷。求：

(1)N点的高度h；
(2)若小滑块向上滑至D点处加速度大小为a，求小滑块与斜面间的摩擦因数μ。

（16分）如图所示，矩形区域MNPQ内有水平向右的匀强电场；在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小为B。半径为R的光滑绝缘空心半圆细管ADO固定在竖直平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN。一质量为m、电荷量为q的带正电小球（可视为质点）从半圆管的A点由静止滑入管内，从O点穿出后恰好通过O点正下方的C点。已知重力加速度为g，电场强度的大小。求：

⑴小球到达O点时，半圆管对它作用力的大小；
⑵矩形区域MNPQ的高度H和宽度L应满足的条件；
⑶从O点开始计时，经过多长时间小球的动能最小？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网