题目内容
 竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环上做圆周运动,如图所示,到达最高点C时的速率vc=
竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环上做圆周运动,如图所示,到达最高点C时的速率vc=
|
分析:因为圆环轨道是光滑的,只有重力做功,所以机械能守恒,可以求得在最低点时的最大速度;
对物体受力分析,根据圆周运动的向心力公式可以求得对轨道的作用力,由周期公式可以知道物体运动的周期.
对物体受力分析,根据圆周运动的向心力公式可以求得对轨道的作用力,由周期公式可以知道物体运动的周期.
解答:解答:解:A、速度最大的点应该是最低点时,根据动能定理:
m
-
m
=2mgR,解得vm=
=
vc,所以A正确.
B、在C点有:mg-T=
,得T=
mg,小球对轨道的作用力向下,所以B错误.
C、整个过程中只有重力做功,机械能守恒,所以C正确.
D、最低点,轨道对小球的支持力与重力的和提供向心力,所以小球对轨道的作用力向下;结合B的方向,所以D正确.
故选:ACD.
| 1 |
| 2 |
| v | 2 m |
| 1 |
| 2 |
| v | 2 c |
|
| 6 |
B、在C点有:mg-T=
m
| ||
| R |
| 1 |
| 5 |
C、整个过程中只有重力做功,机械能守恒,所以C正确.
D、最低点,轨道对小球的支持力与重力的和提供向心力,所以小球对轨道的作用力向下;结合B的方向,所以D正确.
故选:ACD.
点评:小球穿在圆环轨道上做圆周运动,属于杆的模型,在最高点时速度最小,向心力最小,最低点时速度最大,向心力最大,由机械能守恒可以求它们之间的关系.

练习册系列答案
相关题目
 在竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环轨道上做圆周运动,如图所示,到达最高点C时的速率是vC=
在竖直平面内有一个半径为R的光滑圆环轨道,一个质量为m的小球穿在圆环轨道上做圆周运动,如图所示,到达最高点C时的速率是vC=
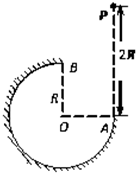 如图所示,在竖直平面内有一个半径为R的圆弧轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力,已知PA=2R,重力加速度为g,则小球( )
如图所示,在竖直平面内有一个半径为R的圆弧轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力,已知PA=2R,重力加速度为g,则小球( ) (2012?安徽)如图所示,在竖直平面内有一个半径为R的圆弧轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力,已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )
(2012?安徽)如图所示,在竖直平面内有一个半径为R的圆弧轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力,已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )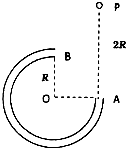 如图所示,在竖直平面内有一个半径为R,粗细不计的圆管轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球恰能沿管道到达最高点B,已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )
如图所示,在竖直平面内有一个半径为R,粗细不计的圆管轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球恰能沿管道到达最高点B,已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )