题目内容
【题目】如图所示,水平放置的平行板电容器极板长度为L,两极板相距为d,距离极板右端也为L处有竖直放置的屏。现有一电荷量为+q、质量为m的带电粒子(重力不计),以初速度v0沿平行于极板方向射入电场中,若电容器不带电粒子打到屏上的O点,现给电容器加入电压等于U的恒定电压,粒子未达到极板上。求:
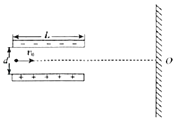
(1)粒子从射入到打到屏上所用的时间;
(2)粒子离开电场时的速度偏转角的正切值;
(3)粒子打到屏上的点P到O点的距离x。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
粒子水平方向不受力的作用,故在水平方向做匀速直线运动,根据x=vt可求得运动时间;根据牛顿第二定律可求得粒子在竖直方向上的位移,根据运动的合成与分解规律可求得竖直方向上的偏转位移和离开电场时的速度,根据三角函数正切值求解;离开电场后粒子做匀速运动,根据运动的合成与分解规律可求得竖直分位移,从而求出粒子在竖直方向上的总位移。
(1)粒子在垂直于电场线的方向做匀速直线运动,所以粒子从射入到打到屏上所有的时间为![]()
(2)设粒子射出电场是沿平行电场线方向的速度为vy,
根据牛顿第二定律,粒子在电场中运动的时间![]()
粒子在电场中的加速度为:![]()
由于![]()
所以![]()
所以粒子离开电场时的速度偏转角的正切值为:![]()
(3)设粒子在电场中偏转距离为y,则![]()
又![]()
解得:![]()

练习册系列答案
相关题目