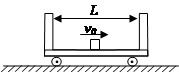��Ŀ����
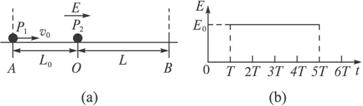
��ͼ��a����ʾ���ڹ⻬��Եˮƽ���AB�����ڴ���ˮƽ���ҵĵ糡���糡ǿ��E��ʱ��ı仯��ͼ��b����ʾ.������ľ�ԵС��P2��ֹ��O��.t=0ʱ���������С��P1���ٶ�v0��A�����AB���������P2�����������������ٶȴ�С����ǰ�� ����P1������Ϊm1,������Ϊq,P2������m2=5m1,A,O���ΪL0��O��B���L=
����P1������Ϊm1,������Ϊq,P2������m2=5m1,A,O���ΪL0��O��B���L= .��֪
.��֪ =
= ,T=
,T=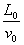 .
.
(1)����ײ��С��P1�����˶��������뼰����ʱ��.
(2)���������ܷ���OB�������ٴη�����ײ.
 ����P1������Ϊm1,������Ϊq,P2������m2=5m1,A,O���ΪL0��O��B���L=
����P1������Ϊm1,������Ϊq,P2������m2=5m1,A,O���ΪL0��O��B���L= .��֪
.��֪ =
= ,T=
,T=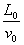 .
.
(1)����ײ��С��P1�����˶��������뼰����ʱ��.
(2)���������ܷ���OB�������ٴη�����ײ.
��1�� ��
�� (2)���ٴ���ײ
(2)���ٴ���ײ
 ��
�� (2)���ٴ���ײ
(2)���ٴ���ײ��1��P1��t1ʱ����P2��ײ����t1= =T
=T
P1,P2��ײ��������P2�ٶ�Ϊv2,�ɶ����غ�
m1v0=m1(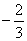 v0)+m2v2
v0)+m2v2
���v2=v0/3(ˮƽ����)
��ײ��С��P1�����˶���������Sm=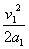
��a1= =
=
���Sm=L0/3
����ʱ��t2=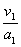 =
=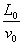 .
.
(2)P2��O���˶���B������ʱ��t2= =4T
=4T
��t2ʱ���ڣ�һֱ���ڵ糡����P1��λ��
x1=v1t2+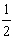 at22=2L
at22=2L
����x1��L������OB֮��P1��P2���ٴ���ײ.
 =T
=TP1,P2��ײ��������P2�ٶ�Ϊv2,�ɶ����غ�
m1v0=m1(
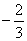 v0)+m2v2
v0)+m2v2���v2=v0/3(ˮƽ����)
��ײ��С��P1�����˶���������Sm=
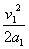
��a1=
 =
=
���Sm=L0/3
����ʱ��t2=
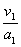 =
=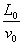 .
.(2)P2��O���˶���B������ʱ��t2=
 =4T
=4T��t2ʱ���ڣ�һֱ���ڵ糡����P1��λ��
x1=v1t2+
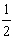 at22=2L
at22=2L����x1��L������OB֮��P1��P2���ٴ���ײ.

��ϰ��ϵ�д�
�����Ŀ
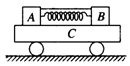
 ����ΪL��С����һ������Ϊ
����ΪL��С����һ������Ϊ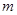 �Ļ���ӳ��ڵװ���������ô�СΪ
�Ļ���ӳ��ڵװ���������ô�СΪ ���ٶȺ����˶����������복�װ�֮��Ķ�Ħ������Ϊ
���ٶȺ����˶����������복�װ�֮��Ķ�Ħ������Ϊ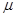 �������복��֮�����ײû��������ʧ�����복�ڵ���ײ������
�������복��֮�����ײû��������ʧ�����복�ڵ���ײ������