题目内容
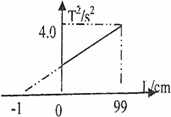某学生用单摆测定重力加速度时，测出多组单摆的摆长l和运动周期T，根据实验数据作出T2-l图象．则①写出由单摆做间谐运动而得到的重力加速度的表达式g=
| 4π2l |
| T2 |
| 4π2l |
| T2 |
9.87
9.87
m/s2．（取π2=9.87）②理论上该实验图象应该是一条过原点的斜线，而该同学由于
在测摆长时未加上小球的半径
在测摆长时未加上小球的半径
，所以得到如图所示的图线，这样通过第一问的方法计算出来的重力加速度与正确操作相比，其结果相同
相同
（填“偏大”、“偏小”、“相同”）分析：（1）由单摆的周期公式式T=2π
可以求出重力加速度的表达式，由图象求出图象的斜率，然后求出重力加速度．
（2）由单摆周期公式的变形公式求出L-T2关系表达式，然后分析图象形成的原因，最后判断测量值与真实值间的关系．
|
（2）由单摆周期公式的变形公式求出L-T2关系表达式，然后分析图象形成的原因，最后判断测量值与真实值间的关系．
解答：解：（1）由单摆周期公式T=2π
可知，g=
；
由T=2π
可得：T2=
l=kl，k=
，
由图象可知：k=
=0.04s2/cm=4s2/m，
由k=
可知，g=
=
=9.87m/s2；
（2）由T=2π
可得：T2=
l=kl，
T2-l图象应该是过原点的直线，
如果测摆长l时，没有包括摆球半径r，
则T2=
（l-r）=
l-
r，
则T2是l的一次函数，而不是正比例函数，
函数图象不是过原点的直线，而是一次函数图象，如图所示；
图象的斜率k与图象是否过原点无关，而g=
，
因此该根据该图象求得的重力加速度与正确操作时求得的重力加速度相同．
故答案为：（1）
；9.87； （2）在测摆长时未加上小球的半径；相同．
|
| 4π2l |
| T2 |
由T=2π
|
| 4π2 |
| g |
| 4π2 |
| g |
由图象可知：k=
| 4.0s2-0s2 |
| 99cm-(-1)cm |
由k=
| 4π2 |
| g |
| 4π2 |
| k |
| 4×9.87 |
| 4s2/m |
（2）由T=2π
|
| 4π2 |
| g |
T2-l图象应该是过原点的直线，
如果测摆长l时，没有包括摆球半径r，
则T2=
| 4π2 |
| g |
| 4π2 |
| g |
| 4π2 |
| g |
则T2是l的一次函数，而不是正比例函数，
函数图象不是过原点的直线，而是一次函数图象，如图所示；
图象的斜率k与图象是否过原点无关，而g=
| 4π2 |
| k |
因此该根据该图象求得的重力加速度与正确操作时求得的重力加速度相同．
故答案为：（1）
| 4π2l |
| T2 |
点评：熟练应用单摆周期公式是正确解题的关键；根据单摆周期公式求出T2-l图象的函数表达式是正确分析实验误差的关键．
练习册系列答案
相关题目
某学生用单摆测定重力加速度时，测出多组单摆的摆长l和运动周期T，根据实验数据作出T2-l图象．则某学生用单摆测定重力加速度，测得数值偏大些，可能是下列哪些原因引起的（ ）
| A、量摆长时没有把小球半径算进去 | B、摆球的质量测得不准确 | C、摆角小，使周期变小 | D、应当测振动30次的时间求其周期，结果把29次当作30次计算周期 |