题目内容
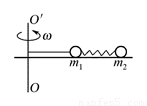
A、B两球质量分别为m1与m2，用一劲度系数为k的弹簧相连，一长为L1的细线与m1相连，置于水平光滑桌面上，细线 的另一端拴在竖直轴OO′ 上，如图所示。当m1与m2均以角速度ω绕OO′ 做匀速圆周运动时，弹簧长度为L2，求：
（1）此时弹簧伸长量；
（2）绳子弹力；
（3）将线突然烧断瞬间A、B两球的加速度大小分别是多少。
【答案】
（1）
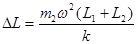（2）
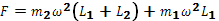（3）
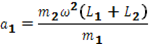
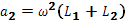
【解析】
试题分析：⑴ 由题意可知，B球受到的弹簧弹力充当B球做圆周运动的向心力。设弹簧伸长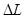
满足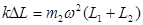 
∴ 弹簧伸长量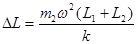
⑵ 对A球分析，绳的弹力和弹簧弹力的合 力充当A球做匀速圆周运动的向心力。
满足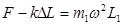 
∴ 绳子的弹力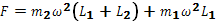
⑶ 绳子烧断的瞬间，A、B两球都由弹簧的弹力提供加速度。
A球：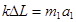
∴
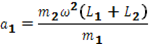
B球：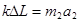 
∴
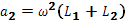
考点：胡克定律、圆周运动
点评：本题考查了圆周运动的向心力来源问题，本题结合弹簧的弹力，利用圆周运动知识建立起向心力与弹力之间的关系，通过向心力来源建立等式。
练习册系列答案
相关题目
A、B两球质量分别为m1与m2，用一劲度系数为K的弹簧相连，一长为l1的细线与m1相连，置于水平光滑桌面上，细线的另一端拴在竖直轴OO′上，如图所示，当m1与m2均以角速度ω绕OO′做匀速圆周运动时，弹簧长度为l2．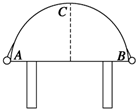
如图所示，A、B两球质量分别为4m和5m，其间用轻绳连接，跨放在光滑的半圆柱体上（半圆柱体的半径为R）．两球从水平直径的两端由静止释放．已知重力加速度为g，圆周率用π表示．当球A到达最高点C时，求：
A、B两球质量分别为m1和m2，用一劲度系数为k的弹簧相连，一长为l1的细线与m1相连，置于水平光滑桌面上，细线的另一端拴在数值轴OO′上，如图所示．当m1与m2均以角速度ω绕OO′做匀速圆周运动且稳定后，弹簧长度为l2．求：
A、B两球之间压缩一根轻弹簧，静置于光滑水平桌面上．已知A、B两球质量分别为2m和m．当用板挡住A球而只释放B球时，B球被弹出落于距桌面水平距离为s的水平地面上，如图，问当用同样的程度压缩弹簧，取走A左边的挡板，将A、B同时释放，B球的落地点距桌面距离为（ ）
在光滑的绝缘水平面上，A、B两球（可以看成质点）位于x轴上，A球带电，B球不带电，开始时B球静置于场强为E＝1×103 N/C的水平匀强电场的边缘（如图1所示），A球从
原点开始经过2s后恰好与B碰撞，碰后合为一体在电场中运动，A、B系统的动能与坐标的部分关系如图2所示，则：