题目内容
18.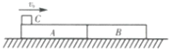 如图所示,A、B两木块靠在一起放在光滑的水平面上,A、B的质量分别为mA=2.0kg和mB=1.5kg.一个质量为mc=0.5kg的小铁块C以v0=8m/s的速度滑到木块A上,离开木块A后最终与木块B一起匀速运动.若木块A在铁块C滑离后的速度为vA=0.8m/s,铁块C与木块A、B间存在摩擦,求:
如图所示,A、B两木块靠在一起放在光滑的水平面上,A、B的质量分别为mA=2.0kg和mB=1.5kg.一个质量为mc=0.5kg的小铁块C以v0=8m/s的速度滑到木块A上,离开木块A后最终与木块B一起匀速运动.若木块A在铁块C滑离后的速度为vA=0.8m/s,铁块C与木块A、B间存在摩擦,求:①铁块C在滑离A时的速度.
②摩擦力对B做的功.
分析 ①对ABC为研究系统,根据动量守恒定律求出铁块C在滑离A时的速度大小.
②对B和C为研究的系统,根据动量守恒定律求出共同的速度,结合功能关系即可求出摩擦力对B做的功.
解答 解:①铁块C在滑离A的过程中,A、B、C系统动量守恒,以C的初速度方向为正方向,由动量守恒定律得:
mCv0=(mA+mB)vA+mCvC,
代入数据解得:vC=2.4m/s;
②铁块C和木块B相互作用最终和B达到相同的速度,铁块C和B作用过程中动量守恒、能量守恒,以C达到初速度方向为正方向,由动量守恒定律得:
mCvC+mBvA=(mC+mB)vB,
由动能定理得:W=$\frac{1}{2}$mBvB2-$\frac{1}{2}$mBvA2,
代入数据解答:W=0.6J,
答:①铁块C在滑离A时的速度为2.4m/s.
②摩擦力对B做的功为0.6J.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程、正确选择研究对象与运动过程、应用动量守恒定律与能量守恒定律即可正确解题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
8.2012年6月24日,“蛟龙”号载人潜水器在西太平洋马里来纳海沟成功突破7000米深度,创造了世界同类潜水器的最大下潜深度.设质量为M的“蛟龙”号所受浮力F始终不变,在运动过程中所受阻力仅与速率有关,重力加速度为g.当“蛟龙”号以某一速率匀速下降时,缆绳的拉力为0;现欲使“蛟龙”号以同样速率匀速率匀速上升,则缆绳的拉力为( )
| A. | 0 | B. | Mg-2F | C. | 2Mg-F | D. | 2(Mg-F) |
13.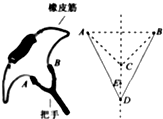 弹弓是80后童年生活最喜爱的打击类玩具之一,其工作原理如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ABC恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标.现将弹丸竖直向上发射,已知E是CD中点,则( )
弹弓是80后童年生活最喜爱的打击类玩具之一,其工作原理如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ABC恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标.现将弹丸竖直向上发射,已知E是CD中点,则( )
 弹弓是80后童年生活最喜爱的打击类玩具之一,其工作原理如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ABC恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标.现将弹丸竖直向上发射,已知E是CD中点,则( )
弹弓是80后童年生活最喜爱的打击类玩具之一,其工作原理如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ABC恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标.现将弹丸竖直向上发射,已知E是CD中点,则( )| A. | 从D到C,弹丸的动能一直在增大 | |
| B. | 从D到C,弹丸的机械能增加 | |
| C. | 从D到C,弹丸的机械能先增大后减小 | |
| D. | 从D到E弹丸增加的机械能大于从E到C弹丸增加的机械能 |
10.关于振动和波的关系,下列说法中正确的是( )
| A. | 如果波源停止振动,在介质中传播的波动也立即停止 | |
| B. | 物体作机械振动,一定产生机械波 | |
| C. | 波的传播速度即波源的振动速度 | |
| D. | 波动的频率,与介质性质无关,仅由波源的振动频率决定 |
7.一定质量的理想气体( )
| A. | 先等压膨胀,再等容降温,其温度必低于起始温度 | |
| B. | 先等温膨胀,再等压压缩,其体积必小于起始体积 | |
| C. | 先等容升温,再等压压缩,其温度有可能等于起始温度 | |
| D. | 先等容加热,再绝热压缩,其内能必大于起始内能 |
8.随着科技的发展,大量的科学实验促进了人们对微观领域的认识,下列说法正确的是( )
| A. | 玻尔建立了量子理论,成功解释了各种原子发光现象 | |
| B. | 德布罗意首先提出了物质波的猜想,而电子衍射实验证实了他的猜想 | |
| C. | 比结合能越大表示原子核中的核子结合得越牢固 | |
| D. | β衰变中产生的β射线是原子核外电子挣脱原子核束缚后形成的 | |
| E. | 一个处于n=4能级的氢原子向低能级跃迁时可能只放出三种不同频率的光子 |
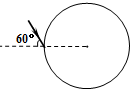 如图所示,一束单色光射入一半径为0.2m玻璃球体,入射角为60°,已知光线在玻璃球内经一次反射后,再次折射回到空气中时与入射光线平行.求:
如图所示,一束单色光射入一半径为0.2m玻璃球体,入射角为60°,已知光线在玻璃球内经一次反射后,再次折射回到空气中时与入射光线平行.求: 已知某电源的电动势不大于6V,为了测定该电源的电动势及内阻,请完成以下题目要求:
已知某电源的电动势不大于6V,为了测定该电源的电动势及内阻,请完成以下题目要求: 如图所示,ABCD为固定在竖直平面内的轨道,AB段平直倾斜且粗糙,BC段是光滑圆弧,对应的圆心角θ=53°,半径为r,CD段平直粗糙,各段轨道均平滑连接,在D点右侧固定了一个$\frac{1}{4}$圆弧挡板MN,圆弧半径为R,圆弧的圆心也在D点.倾斜轨道所在区域有场强大小为E=$\frac{9mg}{5q}$、方向垂直于斜轨向下的匀强电场.一个质量为m、电荷量为q的带正电小物块(视为质点)在倾斜轨道上的A点由静止释放,最终从D点水平抛出并击中挡板.已知A、B之间的距离为2r,斜轨与小物块之间的动摩擦因素为μ=$\frac{1}{4}$,设小物块的电荷量保持不变,重力加速度为g,sin53°=0.8,cos53°=0.6.求:
如图所示,ABCD为固定在竖直平面内的轨道,AB段平直倾斜且粗糙,BC段是光滑圆弧,对应的圆心角θ=53°,半径为r,CD段平直粗糙,各段轨道均平滑连接,在D点右侧固定了一个$\frac{1}{4}$圆弧挡板MN,圆弧半径为R,圆弧的圆心也在D点.倾斜轨道所在区域有场强大小为E=$\frac{9mg}{5q}$、方向垂直于斜轨向下的匀强电场.一个质量为m、电荷量为q的带正电小物块(视为质点)在倾斜轨道上的A点由静止释放,最终从D点水平抛出并击中挡板.已知A、B之间的距离为2r,斜轨与小物块之间的动摩擦因素为μ=$\frac{1}{4}$,设小物块的电荷量保持不变,重力加速度为g,sin53°=0.8,cos53°=0.6.求: