题目内容
1. 如图所示,放在水平面上的斜面体倾角为θ,高度为h,顶端装有小滑轮,斜面体底端有一质量为m的小物体,不计一切摩擦,不可伸长的轻绳一端固定在竖直墙面上的P点(P与斜面体等高),另一端通过滑轮与物体相连.并保持绳与斜面平行,现用水平推力F恰能使斜面体缓慢向右运动.求:
如图所示,放在水平面上的斜面体倾角为θ,高度为h,顶端装有小滑轮,斜面体底端有一质量为m的小物体,不计一切摩擦,不可伸长的轻绳一端固定在竖直墙面上的P点(P与斜面体等高),另一端通过滑轮与物体相连.并保持绳与斜面平行,现用水平推力F恰能使斜面体缓慢向右运动.求:(1)小物体从斜面体底端滑到顶端的位移;
(2)水平推力F的大小.
分析 (1)根据物块沿斜面上滑的位移,结合几何关系求出小物体从底端到顶端的位移大小.
(2)隔离分析,根据共点力平衡求出绳子的拉力,再对整体分析,求出F的大小.
解答 解:(1) 根据几何关系得,小物体从斜面体底端滑到顶端的位移x=$\sqrt{{h}^{2}+(\frac{h}{sinθ}-hcotθ)^{2}}$.
根据几何关系得,小物体从斜面体底端滑到顶端的位移x=$\sqrt{{h}^{2}+(\frac{h}{sinθ}-hcotθ)^{2}}$.
(2)设绳子的拉力为FT,对小物体分析得:
FT=mgsinθ
对斜面和小物体整体有:F=FT,则
F=mgsinθ
答:(1)小物体从斜面体底端滑到顶端的位移为$\sqrt{{h}^{2}+(\frac{h}{sinθ}-hcotθ)^{2}}$;
(2)水平推力F的大小为mgsinθ.
点评 解决本题的关键知道物块的位移由初位置指向末位置,不等于斜面的长度.对于第二问,关键能够正确地受力分析,通过整体和隔离,运用共点力平衡进行求解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.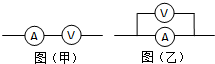 用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )
用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )
 用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )
用相同的灵敏电流计作表头改装成电流表A和电压表V,分别将其串联和并联在一起,然后接入电路中.通电后关于指针的偏角情况的叙述正确的是( )| A. | 图甲中电压表的指针偏角与电流表的相同 | |
| B. | 图甲中电压表的指针偏角比电流表的小 | |
| C. | 图乙中电压表的指针偏角比电流表的大 | |
| D. | 图乙中电压表的指针偏角比电流表的小 |
9.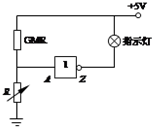 2007年法国科学家阿尔贝•费尔和德国科学家彼得•格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图所示是利用GMR设计的磁铁矿探测仪原理示意图,图中GMR在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是( )
2007年法国科学家阿尔贝•费尔和德国科学家彼得•格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图所示是利用GMR设计的磁铁矿探测仪原理示意图,图中GMR在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是( )
 2007年法国科学家阿尔贝•费尔和德国科学家彼得•格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图所示是利用GMR设计的磁铁矿探测仪原理示意图,图中GMR在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是( )
2007年法国科学家阿尔贝•费尔和德国科学家彼得•格林贝格尔由于发现巨磁电阻(GMR)效应而荣获了诺贝尔物理学奖.如图所示是利用GMR设计的磁铁矿探测仪原理示意图,图中GMR在外磁场作用下,电阻会发生大幅度减小.下列说法正确的是( )| A. | 若存在磁铁矿,则指示灯不亮;调节电阻R的大小,对该探测仪的灵敏度无影响 | |
| B. | 若存在磁铁矿,则指示灯不亮;调节电阻R的大小,对该探测仪的灵敏度有影响 | |
| C. | 若存在磁铁矿,则指示灯亮;调节电阻R的大小,对该探测仪的灵敏度无影响 | |
| D. | 若存在磁铁矿,则指示灯亮;调节电阻R的大小,对该探测仪的灵敏度有影响 |
6.在电磁学发展过程中,许多科学家做出了贡献,下列说法正确的是( )
| A. | 奥斯特发现了电流磁效应;法拉第发现了电磁感应现象 | |
| B. | 麦克斯韦预言了电磁波;楞次用实验证实了电磁波的存在 | |
| C. | 法拉第发现了点电荷的相互作用规律;密立根通过油滴实验测定了元电荷的数值 | |
| D. | 安培发现了磁场对运动电荷的作用规律;洛伦兹发现了磁场对电流的作用规律 |
11. P、Q两点电荷的电场线分布如图所示,c、d为电场中的两点,一个带电粒子(不计重力)从a运动到b的轨迹如图所示,则下列判断正确的是( )
P、Q两点电荷的电场线分布如图所示,c、d为电场中的两点,一个带电粒子(不计重力)从a运动到b的轨迹如图所示,则下列判断正确的是( )
 P、Q两点电荷的电场线分布如图所示,c、d为电场中的两点,一个带电粒子(不计重力)从a运动到b的轨迹如图所示,则下列判断正确的是( )
P、Q两点电荷的电场线分布如图所示,c、d为电场中的两点,一个带电粒子(不计重力)从a运动到b的轨迹如图所示,则下列判断正确的是( )| A. | Q带正电荷 | |
| B. | c点的电势高于d点电势 | |
| C. | b点的电场强度大于a点的电场强度 | |
| D. | 在带电粒子从a点运动到b点的过程中,电场力做负功 |

 质量分别为1kg和4kg的甲、乙两小球,在光滑水平面上迎面相撞,甲球的速率为10m/s,乙球速率为5m/s,碰撞后乙球以1m/s的速率被反向弹回,甲球碰撞后的速度大小为14m/s.
质量分别为1kg和4kg的甲、乙两小球,在光滑水平面上迎面相撞,甲球的速率为10m/s,乙球速率为5m/s,碰撞后乙球以1m/s的速率被反向弹回,甲球碰撞后的速度大小为14m/s.